Strukturierung - Lagebeziehungen bei Ebenen
Lagebeziehungen mit Stützpunkten und Normalenvektoren charakterisieren
Die Tabelle zeigt mögliche Lagebeziehungen von zwei Ebenen. Beachte, dass die Lagebeziehung "schneiden sich orthogonal" ein Spezialfall der Lagebeziehung "schneiden sich" ist.
Gehe davon aus, dass die beiden Ebenen mit einer Ebengleichung in Normalenform gegeben sind. Also: $E_1: [\vec{x} - \vec{p_1}] \cdot \vec{n_1} = 0$ und $E_2: [\vec{x} - \vec{p_2}] \cdot \vec{n_2} = 0$.
| Lagebeziehung | Veranschaulichung | Bedingung |
|---|---|---|
| die Ebenen schneiden sich | 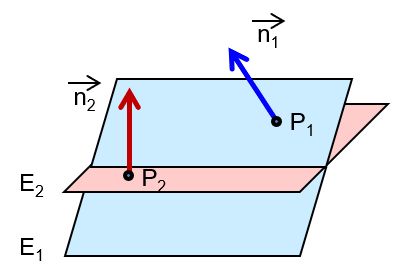 |
|
| die Ebenen schneiden sich orthogonal | 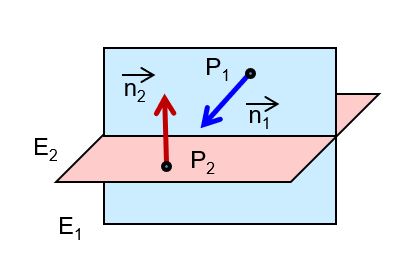 |
|
| die Ebenen sind echt parallel | 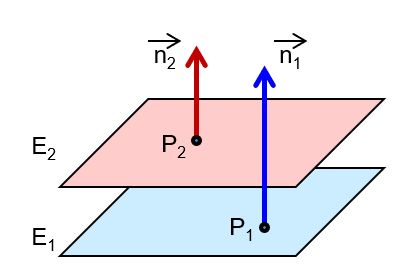 |
|
| die Ebenen sind identisch | 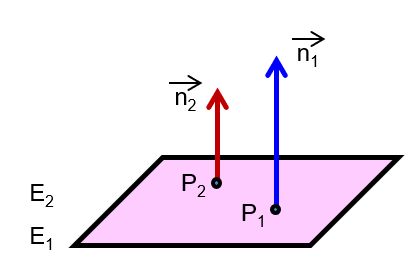 |
Ziel ist es, passende Bedingungen für die jeweiligen Beziehungen zu ergänzen. Bearbeite hierz erst einmal die folgenden Aufgaben. Ergänze abschließend die Bedingungen.
Aufgabe 1
Gegeben ist die Ebene $E_1$ mit einer Ebenengleichung in Normalenform:
$E_1 : \left[\vec{x} - \left(\begin{array}{c} 2 \\ 1 \\ 3 \end{array}\right)\right] \cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) = 0$
Ergänze die Lagebeziehungen der Ebenen $E_1$ und $E_2$ in der Tabelle (mit kurzer Begründung). Überprüfe mit dem Applet (siehe unten).
| Ebene $E_2$ | Lagebeziehung von $E_1$ und $E_2$ | Begründung |
|---|---|---|
| (a) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 3 \\ 0 \\ 0 \end{array}\right)\right] \cdot \left(\begin{array}{c} 4 \\ 0 \\ 2 \end{array}\right) = 0$ | Ebenen sind parallel | $\vec{n_2} = 2\vec{n_1}$; $\vec{n_2}$ und $\vec{n_1}$ sind also parallel; $P_2$ liegt nicht in $E_1$ (überprüft mit einer Punktprobe) |
| (b) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 4 \\ 2 \\ 0 \end{array}\right)\right] \cdot \left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right) = 0$ | ||
| (c) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 2 \\ -1 \\ 4 \end{array}\right)\right] \cdot \left(\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right) = 0$ | ||
| (d) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 3 \\ 1 \\ 1 \end{array}\right)\right] \cdot \left(\begin{array}{c} -2 \\ 0 \\ -1 \end{array}\right) = 0$ | ||
| (e) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 3 \\ 1 \\ 2 \end{array}\right)\right] \cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) = 0$ |
Applet:
Zum Herunterladen: ebene_ebene2.ggb
Aufgabe 2
Ergänze passende Bedingungen in der Tabelle oben. Fasse dir die Ergebnisse in diesem Wissensspeicher zusammen.

