o-mathe | GeoGebra-Applets erstellen » Schieberegler: Dynamische Objekte durch Parametrisierung

Schieberegler: Dynamische Objekte durch Parametrisierung

Für Schieberegler wird eine Zahl in einer Variable gespeichert. Wenn Objekte von dem Wert der Variable abhängen, ändern sie sich bei Änderungen am Schieberegler automatisch mit.

Beispiel: Mit einem Schieberegler wird eine Variable a definiert, die die y-Streckung der Funktion f mit f(x) = a * x^2 steuert.

Beispiel-Applet

Lernaufgabe: Die Funktion $f_{A}$ mit $f_{A} (x) = x^{2} + 1$ ist die um $1$ nach oben verschobene Normalparabel.

(a) Gib Vermutungen für Funktionsgleichungen zu folgendermaßen verschobenen Normalparabeln an:

Funktion	Beschreibung	Funktionsgleichung
$f_{A}$	$1$ nach oben verschoben	$f_{A} (x) = x^{2} + 1$
$f_{B}$	$2$ nach unten verschoben
$f_{C}$	$3$ nach rechts verschoben
$f_{D}$	$4$ nach links verschoben
$f_{E}$	$3$ nach links und $4$ nach oben verschoben
$f_{F}$	$5$ nach unten und $6$ nach rechts verschoben

(b) Das Applet zeigt eine verschobene Normalparabel $g$ mit $g (x) = (x - a)^{2} + b$ . Gib jeweils Werte für die Parameter $a$ und $b$ an, sodass die Funktion $g$ mit den Funktionen $f_{A}$ bzw. $f_{B}$ , $f_{C}$ , … übereinstimmt. Teste jeweils deine Ergebnisse:

Stelle deine Werte für $a$ und $b$ an den Schiebereglern ein.
Vergleiche die Verschiebung der Parabel mit der Beschreibung in (a).

(c) Formuliere die folgende Regel zu Ende:

Die Funktion $g$ mit Funktionsgleichung $g (x) = (x - a)^{2} + b$ entspricht einer Normalparabel mit einer Verschiebung um…

Zum Herunterladen: parabelverschiebung.ggb

Applet nachbauen

Anleitung

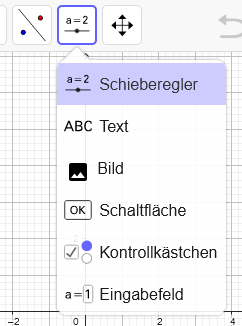
Schieberegler für Variable a anlegen
- Werkzeug Schieberegler auswählen
- Im Hintergrund auf gewünschte Position klicken
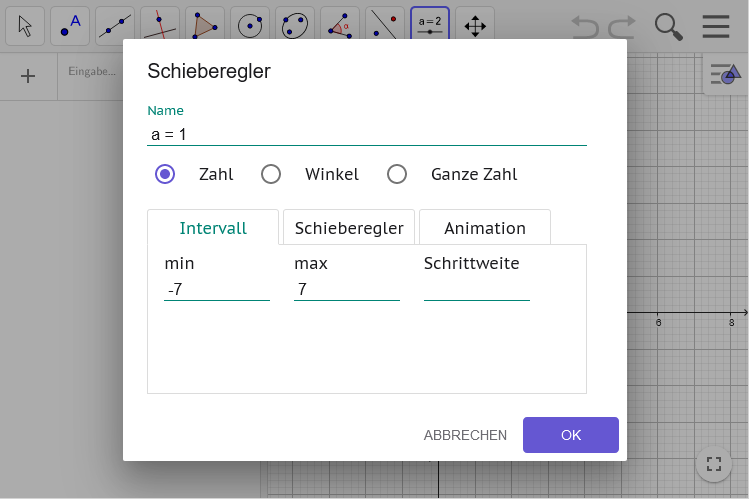
- Namen und Startwert der zugehörigen neuen Variable in Name eingeben (hier: a = 1)
- Wertebereich in min und max eingeben (hier: -7 bis 7)
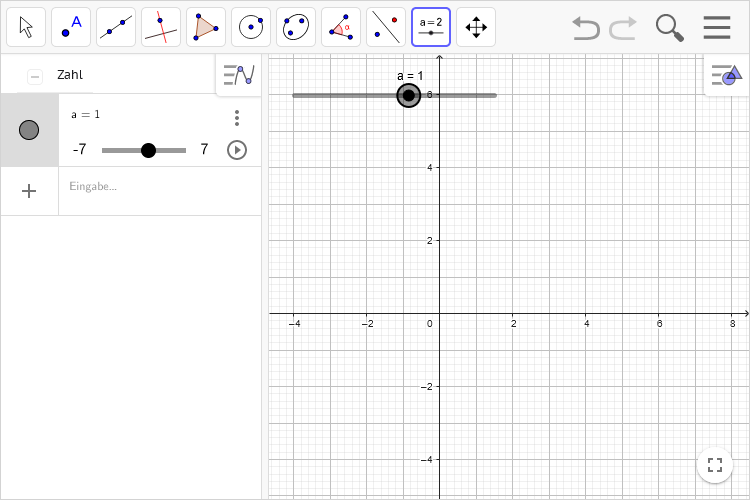
- Auf OK klicken
- Alle Schritte für Variable b wiederholen

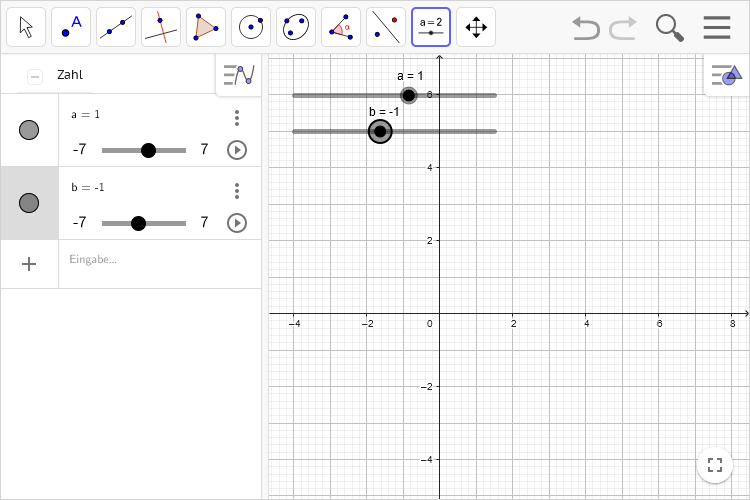
Alle Schritte für Variable b wiederholen

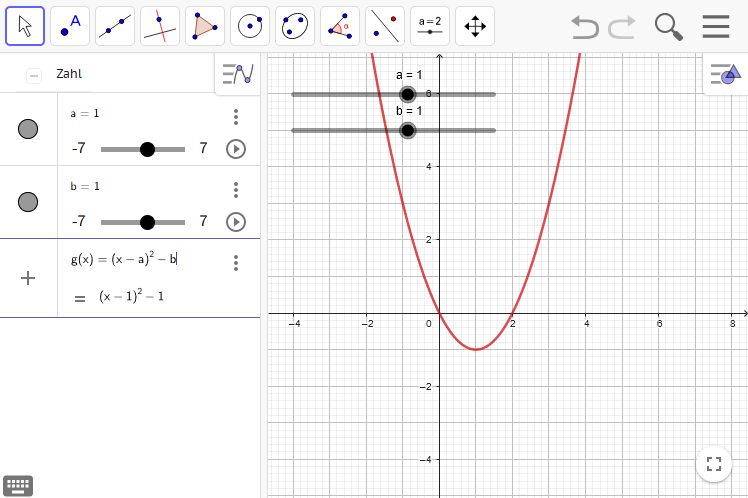
Funktionsgleichung abhängig von Variablen a und b eingeben: g(x) = (x - a)^2 + b

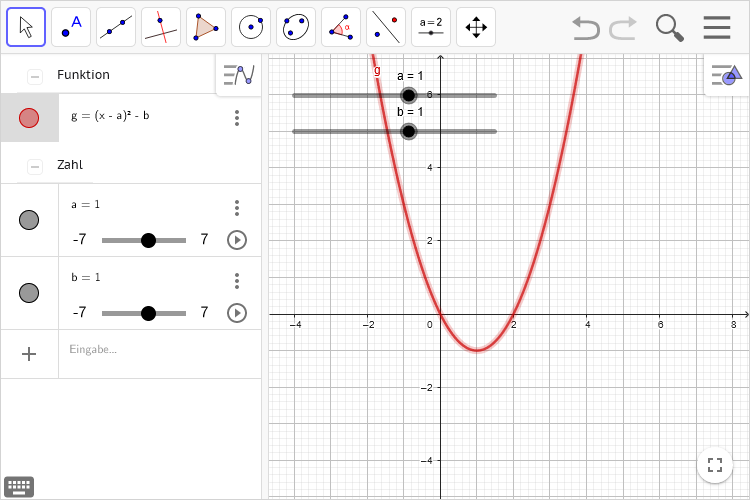
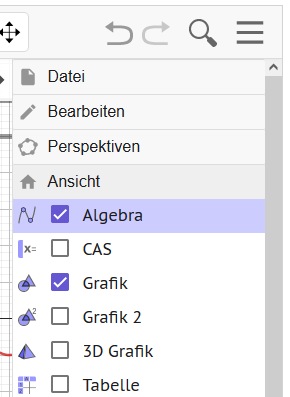
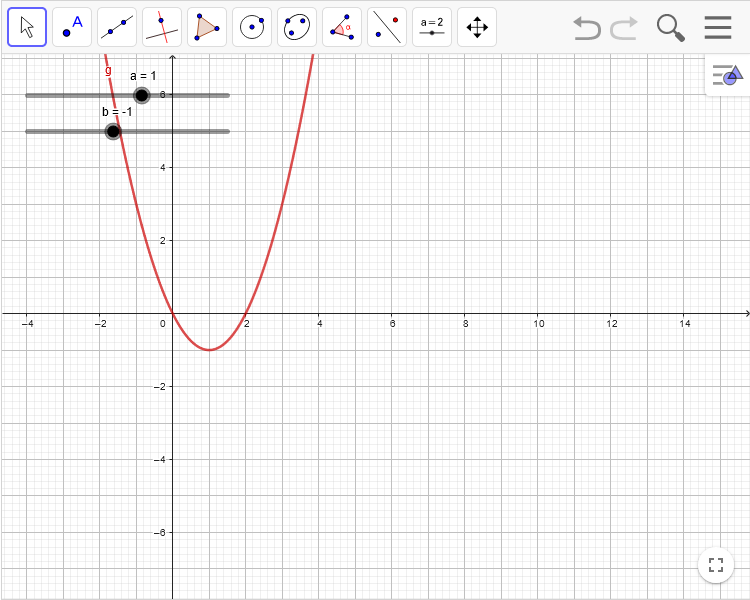
Algebra-Ansicht ausblenden
- Menü oben rechts öffnen
- Untermenü Ansicht
- Haken bei Algebra abwählen
- Menü schließen

Die Einstellungen von Schiebereglern können auch noch nachträglich geändert werden (Rechtsklick → Einstellungen). In den Einstellungen lassen sich auch noch weitere Details ändern (z. B. Farbe, Länge, Ausrichtung horizontal/vertikal).

Formeln können auch direkt mit Parametern eingegeben werden. Dann werden automatisch Schieberegler für alle Parameter erzeugt. Es muss nur in der Regel noch im Nachhinein der Wertebereich geändert werden.

Mögliche Erweiterungen

Schrittweite des Schiebereglers einstellen
Wie im Beispielapplet das Gitter anpassen:
- Rechtsklick auf Hintergrund
- Grafik
- Koordinatengitter
- Art des Koordinatengitters, ggf. Abstand wählen
Optional einblendbare Normalparabel und Visualisierung der Verschiebung zum besseren Vergleichen (→ Hilfen und Kontrollen)

Um das Ergebnis zu speichern:

Menü oben rechts öffnen
Auf dem Computer speichern

Andere Projekte

Punkt entlang eines Funktionsgraphen bewegen

Eine Funktion f definieren
Parametrisierten Punkt P = (a, f(a)) erzeugen
Vertikale Verbindung zur x-Achse zeigen: Strecke((a, 0), (a, f(a)))

Erkundung trigonometrischer Funktionen

Punkt P = (sin(a), cos(a)) per Schieberegler auf dem Einheitskreis entlang drehen
Hilfspunkt Q = (sin(a), 0) einführen, Sinus und Kosinus als Verbindungsstrecken mit diesem Punkt visualisieren
Gleichzeitig an trigonometrischer Funktion visualisieren
- Grafik 2 aktivieren
- Punkt Q = (a, cos(a)) definieren
- Punkt nur in Grafik 2 sichtbar machen (Rechtsklick → Einstellungen → Anzeigen in)
- Im Rechtsklickmenü des Punkts die Spur aktivieren
- Funktion in Grafik 2 zeigen, ggf. nur per Kontrollkästchen aktivieren