Übungen - Modellierung von Austauschprozessen

Aufgabe 1

Ein Sharing-System werde mit folgendem Übergangsgraphen beschrieben.

Übergangsgraph	Übergangstabelle	Prozessmatrix
	von A von B von C zu A $\dots$ $\dots$ $\dots$ zu B $\dots$ $\dots$ $\dots$ zu C $\dots$ $\dots$ $\dots$	$P = \begin{pmatrix} \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots \end{pmatrix}$

(a) Überprüfe, ob der Übergangsgraph einen Austauschprozess beschreibt. Kontrolliere hierzu, ob die Gesamtanzahl der Objekte eines vorgegebenen Objektbestandes gleich bleibt.

(b) Ergänze die Übergangstabelle und bestimme mit ihr die Prozessmatrix $P$.

(c) Starte mit der in der folgenden Übersicht angegebenen Anfangsverteilung. Berechne für $2$ Schritte den jeweils nächsten Verteilungsvektor. Für $\vec{v}_2$ ist ein Kontrollwert angegeben.

Schritte	Berechnung des Verteilungsvektors
$0$	$\vec{v}_0 = \begin{pmatrix} 100 \\ 0 \\ 100 \end{pmatrix}$
$1$	$\vec{v}_1 = \dots$
$2$	$\vec{v}_2 = \dots = \begin{pmatrix} \cdots \\ 100 \\ \cdots \end{pmatrix}$

(d) Verteilungen kann man auch mit relativen Häufigkeitsangaben bestimmen. Berechne in der folgenden Übersicht die fehlenden Werte.

Schritte	Berechnung des Verteilungsvektors
$0$	$\vec{v}_0 = \begin{pmatrix} 0.5 \\ 0.2 \\ 0.3 \end{pmatrix}$
$1$	$\vec{v}_1 = \dots$
$2$	$\vec{v}_2 = \dots = \begin{pmatrix} 0.66 \\ \cdots \\ \cdots \end{pmatrix}$

Aufgabe 2

Am 01.01.2002 wurde der Euro als neue gemeinschaftliche Zahlungseinheit eingeführt. Jedes beteiligte Land kann selbst in einem festgelegten Umfang Euro-Münzen und Euro-Scheine in Umlauf bringen. Die Münzen und Scheine sind dann in allen am Euro-Raum beteiligten Ländern gültig.

Wir betrachten hier die Münzwanderungen von in Deutschland geprägten 1-Euro-Münzen in die Euro-Auslandzone (das sind alle Länder außer Deutschland, in denen der Euro auch eingeführt ist) und wieder zurück.

Wir gehen dabei von folgenden Modellannahmen aus:

• Die Gesamtanzahl der in Deutschland geprägten 1-Euro-Münzen, die im gesamten Euro-Raum im Umlauf sind, ist stets gleich.
• Die Übergangsraten pro Jahr zur Wanderung von in Deutschland geprägten 1-Euro-Münzen von Deutschland ins Euro-Ausland und wieder zurück bleiben gleich.

(a) Inwieweit sind diese Modellannahmen in der Realität tatsächlich erfüllt? Stelle Vermutungen hierzu auf. Infos über die Gesamtanzahl der 1-Euro-Münzen findet man in diesem Dokument der Bundesbank. Infos zur Durchmischung von Euro-Münzen gibt es in diesem Dokument der Bundesbank.

(b) Wir gehen hier von folgenden (hier frei gewählten) Daten aus:

• Jährlich wandern $4 \%$ der in Deutschland befindlichen 1-Euro-D-Münzen ins Euro-Ausland. Die restlichen 1-Euro-D-Münzen verbleiben in Deutschland.
• Jährlich wandern $5 \%$ der im Euro-Ausland befindlichen 1-Euro-D-Münzen wieder nach Deutschland. Die restlichen 1-Euro-D-Münzen verbleiben im Euro-Ausland.

Beschreibe die Münzwanderungen mit einem Übergangsgraph und einer Übergangstabelle.

(c) Gehe davon aus, dass bei der Euro-Einführung 2002 alle geprägten 1-Euro-D-Münzen in Deutschland ausgegeben wurden. Berechne (ohne Hilfsmittel) im betrachteten Münzwanderungsmodell, wie groß der Anteil der 1-Euro-D-Münzen in den Folgejahren (2003 .. 2005) ist.

(d) Erkläre, wie man (im betrachteten Münzwanderungsmodell) den derzeitigen Anteil der 1-Euro-D-Münzen in Deutschland und im Euro-Ausland berechnet. Die Berechnungen kannst du mit ProSiTo durchführen.

Aufgabe 3

In dieser Aufgabe geht es um Migrationsprozesse. Wir betrachten hierzu folgende konstruierte Situation:

Eine Oberstufenparty findet in 4 großen Hallen statt, die wie in der Abbildung angeodnet sind. Zwischen benachbarten Hallen kann man sich hin und her bewegen.

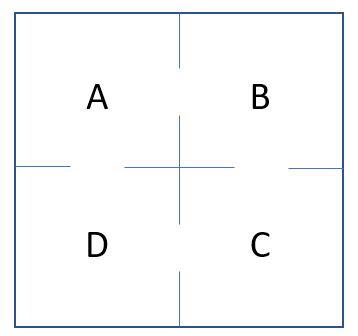
In jedem Raum gibt es Musik einer bestimmten Musikrichtung. Der Mathekurs beobachtet das Verhalten der Partygäste und erstellt ausgehend von den Beobachtungen das folgende vereinfachte Verhaltensmodell:

• Die Gesamtanzahl der Partygäste wird als konstant vorausgesetzt.
• Die gespielten Songs dauern alle (in etwa) gleich lang.
• Nach jeder Song verbleiben nur $20 \%$ der Gäste im Raum A. Alle anderen wechseln mit jeweils $40 \%$ in die Räume B und D.
• Nach jedem Song verbleiben $60 \%$ der Gäste im Raum B. Alle anderen wechseln mit jeweils $20 \%$ in die Räume A und C.
• Nach jedem Song verbleiben $40 \%$ der Gäste im Raum C. Alle anderen wechseln mit jeweils $30 \%$ in die Räume B und C.
• Nach jedem Song verbleiben $80 \%$ der Gäste im Raum D. Alle anderen wechseln mit jeweils $10 \%$ in die Räume A und C.

Anhand dieser Daten erkennt man auf den ersten Blick, dass die Musik in Raum D am beliebtesten ist. Aber, wie verteilen sich die Partygäste im Laufe der Zeit auf die verschiedenen Räume? Genau das sollst du in den folgenden Aufgaben mit mathematischen Mitteln herausfinden.

(a) Welche Modellannahmen werden im Verhaltensmodell gemacht. Inwieweit sind sie realistisch? Warum muss man für Vorhersagen meist solche vereinfachenden Annahmen treffen?

(b) Beschreibe das Verhaltensmodell mit Hilfe eines Übergangsgraphen. Du kannst den Graph im Simulationstool ProSiTo erstellen.

(c) Betrachte die Ausgangsverteilung $\vec{v}_0 = \begin{pmatrix} 400 \\ 0 \\ 0 \\ 0 \end{pmatrix}$. Berechne die Verteilung nach einem Simulationsschritt. Vergleiche mit dem Ergebnis, das ProSiTo liefert.

Aufgabe 4

Vorgegeben ist die Matrix $P = \begin{pmatrix} a & 1-b \\ 1-a & b \end{pmatrix}$. Die Parameter $a$ und $b$ stehen hier für reelle Zahlen mit $0 \text{ < } a, b \text{ < } 1$.

(a) Begründe, dass $P$ mit den Vorgaben für die Parameter $a$ und $b$ eine stochastische Matrix ist.

(b) Die Matrix $P$ wird als Prozessmatrix für einen Austauschprozess betrachtet. Erstelle einen passenden Übergangspraph zu dieser Prozessmatrix (mit den Kontenbezeichnern A und B).

(c) Zeige, dass $P^2 = \begin{pmatrix} a^2+(1-b)(1-a) & a(1-b)+(1-b)b \\ (1-a)a+b(1-a) & (1-a)(1-b)+b^2 \end{pmatrix}$.

(d) Deute die Elemente der Matrix $P^2$ wie in der folgenden Übersicht. Ergänze die Übersicht.

Element	Deutung	Prozessschritte
$a^2+(1-b)(1-a)$	von A nach A in $2$ Schritten	$A \stackrel{a}{\longrightarrow} A \stackrel{a}{\longrightarrow} A$ $A \stackrel{1-a}{\longrightarrow} B \stackrel{1-b}{\longrightarrow} A$
$a(1-b)+(1-b)b$
$(1-a)a+b(1-a)$
$(1-a)(1-b)+b^2$