Entwicklung von Simulationsmodellen

Einordnung und Zielsetzung

Nach dem empirischen Gesetz der großen Zahlen lässt sich jede Wahrscheinlichkeit (näherungsweise) bestimmen, indem das zu Grunde liegende Zufallsexperiment (hinreichend oft) wiederholt ausgeführt wird. So erhält man ein universelles Verfahren zur Bestimmung von Wahrscheinlichkeiten. Das Verfahren stößt an seine Grenzen, wenn eine wiederholte Ausführung des betrachteten Zufallsexperiments nicht möglich oder zu aufwändig ist. Hier kann dann eine Simulation des Zufallsexperiments weiterhelfen. Das betrachtete Zufallsexperiment wird mit einem leicht durchführbaren Zufallsexperiment strukturgetreu nachgebildet.

Die Grundidee des Simulationsansatzes wird bereits in der Sekundarstufe I erarbeitet und in einfachen Fällen beim Problemlösen genutzt. Ziel des Kapitels Simulation von Zufallsexperimenten ist es, das Verfahren in komplexeren Anwendungssituationen anzuwenden und dabei den Modellierungsprozess reflektierend zu vollziehen. Ein besonderer Fokus liegt dabei in der automatisierenden Ausführung und Auswertung des Simulationsvorgangs. Folgende Zielsetzungen stehen dabei im Vordergrund:

Hier lernst du, ...

• ... wie man Zufallsexperimente mit Hilfe einfacher Zufallsgeräte simulieren kann.
• ... wie Zufallszahlengeneratoren zur Simulation von Zufallsexperimenten verwendet werden.
• ... was bei der Entwicklung von Simulationsmodellen beachtet werden muss.

Progression bei der Wahl der Simulationsmittel

Bei der Wahl der Simulationsmittel werden im Kapitel Simulation von Zufallsexperimenten verschiedene Möglichkeiten vorgestellt.

• enaktiver Ansatz: Wir verwenden einfache Zufallsgeräte (wie Würfel und Münzen) bei der Konstruktion des Simulationsmodells und führen die Simulation mit diesen Geräten händisch durch.
• halbautomatisierter Ansatz mit erzeugbaren Zufallszahlen: Wir nutzen vorgegenbene Sammlungen von Zufallszahlen. Statt Blöcken mit Zufallsziffern (die dann erst einmal in geeignete Blöcke von Zufallszahlen umgewandelt werden müssen) verwenden wir ein Tool, das problemangepasste Blöcke von Zufallszahlen generiert. Die Auswertung muss dann noch händisch durchgeführt werden.
• automatisierter Ansatz mit programmierter Erzeugung der Zufallszahlen und deren Auswertung: Wir nutzen ein Tabellenkalkulationsprogramm als Programmiersystem, um problemangepasste Blöcke von Zufallszahlen zu generieren und sie zielorientiert auszuwerten.

Die folgenden Ausführungen verdeutlichen diese Ansätze an einem einfachen Simationsbeispiel.

Simulation mit einfachen Zufallsgeräten

Die Übersicht verdeutlicht die Ausgangssituation und den gewählten enaktiven Simulationsansatz.

Beschreibung der Ausgangssituation

Beschreibung des Simulationsmodells

Zufallsexperiment: Den Krankenstand von $8$ Spielerinnen zu einem Zeitpunkt ermitteln. Beobachtet wird die Anzahl der erkrankten Spielerinnen. Annahme: Der Krankenstand der Spielerinnen entspricht dem Krankenstand $1/3$ in der Bevölkerung. Es findet z.B. keine gegenseitige Ansteckung der Spielerinnen statt, die zu einem erhöhten Krankenstand führt. Spielerinnen, die nicht krank sind, fehlen nicht aus anderen Gründen. Struktur: Es handelt sich um ein $8$-stufiges Zufallsexperiment. In jeder Stufe beträgt die Wahrscheinlichkeit für „krank“ genau $1/3$. Gesuchte Wahrscheinlichkeit: Wie groß ist die Wahrscheinlichkeit, dass mindestens $4$ Spielerinnen erkrankt sind?

Zufallsexperiment: Einen Würfel $8$-mal werfen. Beobachtet wird, ob $1,2$ (entspricht krank) oder $3,4,5,6$ (entspricht nicht krank) geworfen wird. Struktur: Es handelt sich um ein $8$-stufiges Zufallsexperiment. In jeder Stufe beträgt die Wahrscheinlichkeit für das Ereignis „$1$ oder $2$“ genau $1/3$. Gesuchte Wahrscheinlichkeit: Wie groß ist die Wahrscheinlichkeit, dass man mindestens $4$-mal das Ereignis „$1$ oder $2$“ erhält? Abschätzung der Wahrscheinlichkeit: Wiederholte Durchführung des Zufallsexperiment: hier $100$-mal.

Simulation mit problemangepasster Erzeugung von Zufallszahlen

Mit dem folgenden Zufallszahlengenerator können nach eigenen Einstellungen Blöcke von Zufallszahlen erzeugt werden.

Folgende Einstellungen eignen sich z.B. zur Simulation im betrachteten Problemkontext.

• Mit [Minimum: 1] und [Maximum: 3] wird der Bereich eingestellt, in dem die Zufallszahlen liegen. Wir nutzen z.B. die Codierung 1: erkankt und 2,3: nicht erkankt.
• Mit [Größe des Blocks: 8] wird festgelegt, das wir den Krankenstand von 8 Spielerinnen simulieren.
• Mit [Anzahl der Blöcke: 100] wird festgelegt, dass das Zufallsexperiment den Krankenstand von $8$ Spielerinnen zu einem Zeitpunkt ermitteln 100-mal simuliert werden soll.
• Die Einstellung [Wiederholte Werte erlauben: ja] legt fest, dass eine Zufallszahl in einem Block wiederholt vorkommen kann.
• Die Einstellung [Reihenfolge der Werte verwerfen: ja] führt dazu, dass die erzeugten Zufallszahlen sortiert dargestellt werden.

Wenn jetzt [Daten generieren] aktiviert wird, erhält man eine Liste mit passend generierten Zufallszahlen, die leicht händisch ausgewertet werden können.

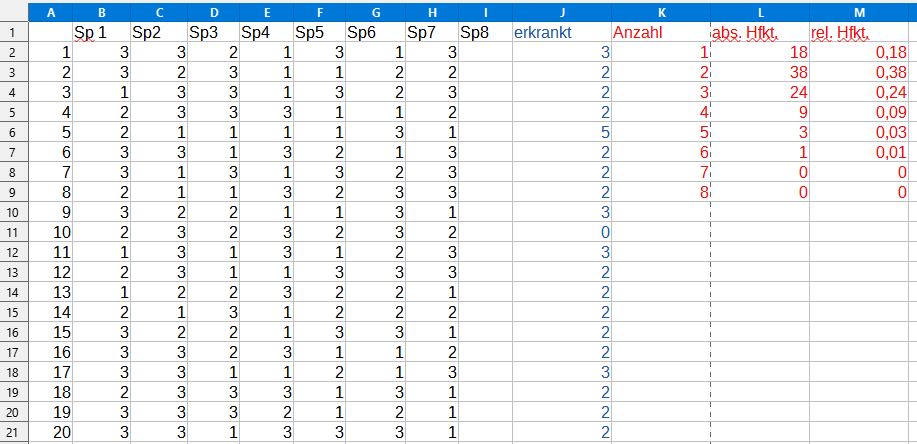
Simulation mit einem programmierbaren Tabellenkalkulationsprogramm

Mit dem Zufallszahlengenerator (s.o) können für viele Problemsituationen passende Zufallszahlen erzeugt werden. Die Auswertung muss aber selbst übernommen werden. Beides – Erzeugung von Zufallszahlen und Auswertung der erzeugten Zufallszahlen – lässt sich flexibel mit einem Tabellenkalkulationsprogramm durchführen.

Die Abbildung zeigt einen Ausschnitt aus den erzeugten Daten bei 100 Simulationen zum Krankenstand von 8 Spielerinnen.

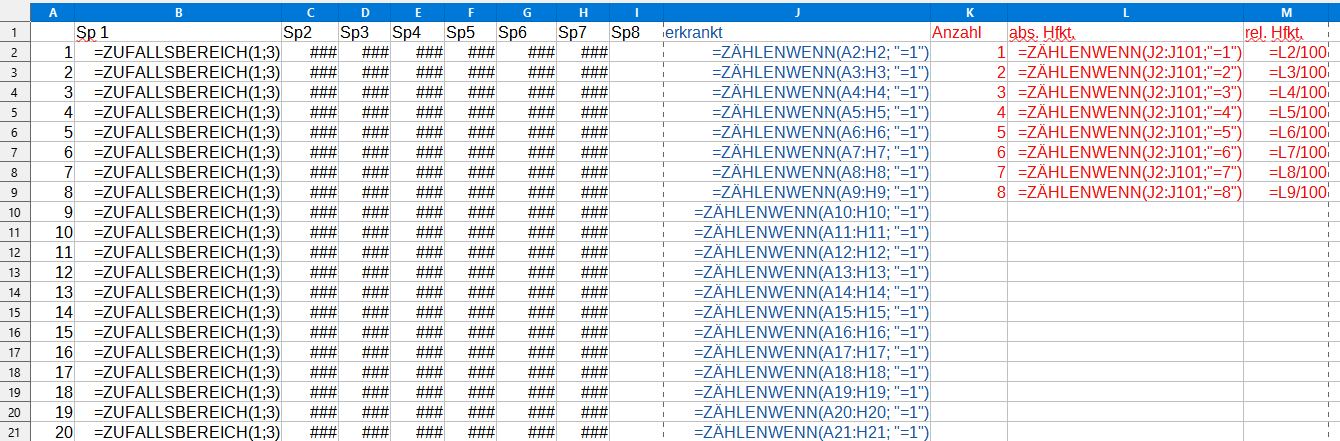
Die zu Grunde liegenden Berechnungsformeln werden hier (teilweise) angezeigt.

Eine Simulation mit einem Tabellenkalkulationsprogramm entlastet von der händischen Auswertung der erzeugten Zufallszahlen. Sie erfordert allerdings, dass die generierten Zufallszahlen mit geeigneten Formeln ausgewertet werden. Hierfür müssen passende im Tabellenkalkulationsprogramm vordefinierte Funktionen verwendet werden. Eine Einarbeitung in die Programmierlogik eines Tabellenkalkulationsprogramms ist somit erforderlich.

Die Progression bei der Wahl der Simulationsmittel – von einfachen Zufallsgeräten bis hin zur programmierbaren Tabellenkalkulation – ist mit einer Entlastung bei der Durchführung der Simulation und mit einer Steigerung der Komplexität bei der Modellierung verbunden. Im Kapitel Simulation von Zufallsexperimenten lassen wir offen, welcher Ansatz im Unterricht gewählt wird.