Zusammenfassung - Folgenkonzept
Zahlenfolgen in Kontexten
Zahlenfolgen kommen in verschieden Kontexten vor. Hier zwei Beispiele:
Beispiel: $0; 1; 3; 6; 10; ...$
Die Zahlenfolge $0; 1; 3; 6; 10; ...$ beschreibt der Reihe nach die jeweilige Anzahl von Begrüßungen, wenn $1; 2; 3; 4; 5; ...$ Personen sich alle gegenseitig begrüßen.
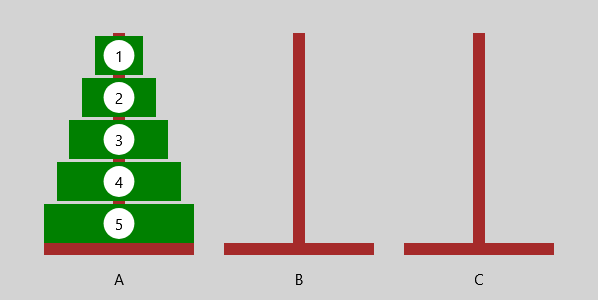
Beispiel: $0; 0.5; 1; 1.5; 2; ...$
Die Zahlenfolge $0; 0.5; 1; 1.5; 2; ...$ beschreibt der Reihe nach den Gesamtinhalt eines Sparschweins [in €] nach $0; 1; 2; 3; 4; 5; ...$ Tagen, wenn das Sparschwein zu Beginn leer ist und man jeden Tag 0.50 € hineinwirft.
Mathematische Beschreibung der Beispielfolgen
Zahlenfolgen können mathematisch mit Hilfe von Funktionen beschrieben werden. Wir verdeutlichen das anhand der betrachteten Beispiele.
Beispiel: $0; 1; 3; 6; 10; ...$
Zum Herunterladen: folge_als_funktion1.ggb
Die Zahlenfolge wird mit einer Funktion beschrieben, die einer natürlichen Zahl $n$ aus dem Bereich $n = 1; 2; 3; ...$ die Zahl $a_n$ zuordnet, die so berechnet wird:
$a_n = \displaystyle{\frac{n \cdot (n-1)}{2}}$ für $n = 1; 2; 3; ...$
Beispiel: $0; 0.5; 1; 1.5; 2; ...$
Zum Herunterladen: folge_als_funktion2.ggb
Die Zahlenfolge wird mit einer Funktion beschrieben, die einer natürlichen Zahl $n$ aus dem Bereich $n = 0; 1; 2; 3; ...$ die Zahl $a_n$ zuordnet, die so berechnet wird:
$a_n = n \cdot 0.5$ für $n = 0; 1; 2; 3; ...$
Präzisierung des Folgenbegriffs
Die Beispiele verdeutlichen, dass wir eine Zahlenfolge als Funktion auffassen können.
Eine Folge ist eine Funktion, die jeder natürlichen Zahl (aus einer unendlichen Menge natürlicher Zahlen) eine reelle Zahl zuordnet.
- Die Definitionsmenge einer Folge ist eine unendliche Menge natürlicher Zahlen. Meist ist es die Menge $\mathbb{N} = \{ 0, 1, 2, ... \}$ oder die Menge $\mathbb{N}^{*} = \{ 1, 2, ... \}$. Wir beschreiben die Definitionsmenge oft in der Form $n = 0; 1; 2; ...$ bzw. $n = 1; 2; ...$.
- Die Folgenglieder einer Folge sind die Funktionswerte der entsprechenden Funktion. Wir bezeichnen sie mit z.B. mit $a_1; a_2; a_3; ...$. Hier wird das Folgenglied mit der Platznummer $n$ mit dem Bezeichner $a_n$ versehen.
- Die Folgenglieder einer Folge können beliebige reelle Zahlen sein.
- Die Folgenglieder kann man - wie bei Funktionen üblich - im Koordinatensystem verdeutlichen. Beachte, dass der Graph einer Folge nur aus unverbundenen Punkten besteht.
- Eine Folge wird - etwas ungewohnt - nicht wie bei Funktionen üblich mit einem Bezeichner wie z.B. $a$ beschrieben. Stattdessen benutzt man einen Ausdruck wie z.B. $\left( a_n \right)$, wenn man die Folge mit den Folgengliedern mit $a_1; a_2; a_3; ...$ beschreibt.
Darstellung von Folgen
Zur Darstellung von Folgen nutzt man in der Regel explizite oder rekursive Berechnungsvorschriften. Wir verdeutlichen die verschiedenen Arten zur Festlegung der Berechnungen anhand der Beispiele von oben.
Beispiel: $0; 1; 3; 6; 10; ...$
Die Folgenglieder $a_1; a_2; a_3; ...$ lassen sich mit einer expliziten Darstellung so berechnen:
$a_n = \displaystyle{\frac{n \cdot (n-1)}{2}}$ für $n = 1; 2; 3; ...$
Die Berechnung eines Folgenglieds ist direkt aus der Platznummer möglich.
$a_1 = (1 \cdot 0)/2$
$a_2 = (2 \cdot 1)/2$
$a_3 = (3 \cdot 2)/2$
...
Die Folgenglieder $a_1; a_2; a_3; ...$ lassen sich alternativ mit einer rekursiven Darstellung so berechnen:
$a_1 = 0$
$a_{n+1} = a_n + n$ für $n = 1; 2; 3; ...$
Die Berechnung eines Folgenglieds greift auf bereits vorher berechnete Folgenglieder zurück.
$a_1 = 0$
$a_2 = a_1 + 1$
$a_3 = a_2 + 2$
...
Beispiel: $0; 0.5; 1; 1.5; 2; ...$
Die Folgenglieder $a_0; a_1; a_2; ...$ lassen sich mit einer expliziten Darstellung so berechnen:
$a_n = n \cdot 0.5$ (für $n = 0; 1; 2; ...$)
Die Berechnung eines Folgenglieds ist direkt aus der Platznummer möglich.
$a_0 = 0 \cdot 0.5$
$a_1 = 1 \cdot 0.5$
$a_2 = 2 \cdot 0.5$
...
Die Folgenglieder $a_0; a_1; a_2; ...$ lassen sich alternativ mit einer rekursiven Darstellung so berechnen:
$a_0 = 0$
$a_{n+1} = a_n + 0.5$ für $n = 0; 1; 2; ...$
Die Berechnung eines Folgenglieds greift auf bereits vorher berechnete Folgenglieder zurück.
$a_0 = 0$
$a_1 = a_0 + 0.5$
$a_2 = a_1 + 0.5$
...
