Übungen - Monotonie und Beschränktheit
Aufgabe 1
Gib bei den Folgen unten die jeweiligen Eigenschaften an. Du kannst diese Abkürzungen benutzen.
- A: Die Folge ist streng monoton steigend.
- B: Die Folge ist monoton steigend.
- C: Die Folge ist streng monoton fallend.
- D: Die Folge ist monoton fallend.
- E: Die Folge ist monoton.
- F: Die Folge ist nach oben beschränkt.
- G: Die Folge ist nach unten beschränkt.
- H: Die Folge ist beschränkt.
| Aufgabe | Folge | Eigenschaften |
|---|---|---|
| (a) | $a_n = \displaystyle{\frac{1}{n}}$ für $n = 1; 2; 3; ...$ | ... |
| (b) |
$a_1 = 0$ $a_{n+1} = a_n - 2$ für $n = 1; 2; 3; ...$ |
... |
| (c) | $\left( a_n \right)$: $1; 2; 2; 3; 3; 3; 4; 4; 4; 4; ...$ | ... |
| (d) |
$a_1 = 1$ $a_{n+1} = (-1) \cdot a_n$ für $n = 1; 2; 3; ...$ |
... |
| (e) | $a_n = (-1)^n \cdot n$ für $n = 1; 2; 3; ...$ | ... |
| (f) | $\left( a_n \right)$: $1; 4; 9; 16; 25; ...$ | ... |
| (g) | $a_n = 4 - \displaystyle{\frac{1}{n}}$ für $n = 1; 2; 3; ...$ | ... |
Aufgabe 2
Wir wollen im vorgeheizten Backofen (180°C ) eine Tiefkühl-Pizza (-20°C ) aufbacken. Dafür haben wir zwei Ofen zur Verfügung:
Brutzler 9000: Jede Minute erhöht sich die Temperatur der hineingestellten Lebensmittel um 25°C , bis die Temperatur des Backofens erreicht ist.
Backomat: Die Temperaturdifferenz der hineingestellten Lebensmittel und des Backofens halbiert sich jede Minute.
(a) Erstelle eine Wertetabelle (für beide Backöfen), in der die erreichten Temperaturen der ersten zehn Minuten eingetragen sind.
(b) Zeichne die Graphen der beiden Folgen mit verschiedenen Farben in ein gemeinsames Koordinatensystem.
(c) Beschreibe das Verhalten der beiden Folgen mit passenden Fachbegriffen.
(d) (für Experten) Beschreibe die Folgen mit einer rekursiven und / oder expliziten Folgendarstellung. Begründe mit diesen Darstellungen die Eigenschaften der Folgen.
Aufgabe 3 (für Expertinnen und Experten)
In dieser Aufgabe geht es um den Flächeninhalt und den Umfang einer Quadratpflanze.
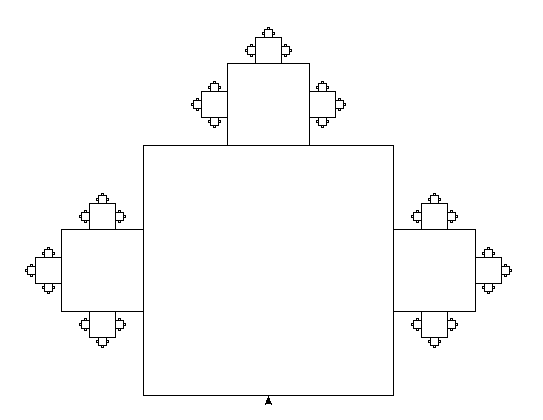
(a) Benutze das folgende Programm, um Quadratpflanzen zu zeichnen. Wenn du das grüne Dreieck anklickst, dann beginnt die Turtle mit dem Zeichnen.
Voreingestellt ist im Quelltext die Anweisung quadratpflanze(2, 200). Hier wird die 2. Quadratpflanze
mit einer Grundlänge von 200 Pixeln gezeichnet. Teste auch diese Anweisungen: quadratpflanze(1, 200) und
quadratpflanze(3, 200). Du kannst die Veränderungen direkt im Quelltext vornehmen und musst dann nur
nochmal das Programm mit dem grünen Dreieck neu starten.
(b) Die Folge $\left( A_n \right)$ beschreibt den Flächeninhalt der $n$-ten Quadratpflanze. Wir gehen dabei von einer Länge $1$ der Grundseite aus. Es gilt demnach $A_1 = 1$.
Bestimme $A_2$ und $A_3$. Entwickle auch eine allgemeine (rekursive) Berechnungsformel.
Die Folge $\left( A_n \right)$ ist streng monoton steigend und nach oben beschränkt. Begründe diese Eigenschaften anschaulich.
(c) Die Folge $\left( u_n \right)$ beschreibt den Umfang der $n$-ten Quadratpflanze. Wir gehen dabei von einer Länge $1$ der Grundseite aus. Es gilt demnach $u_1 = 4$.
Bestimme $u_2$ und $u_3$. Was fällt auf? Entwickle auch eine allgemeine Berechnungsformel.
Die Folge $\left( u_n \right)$ ist streng monoton steigend und nicht nach oben beschränkt. Begründe diese Eigenschaften mit Hilfe der Berechnungsformel.

