Fibonacci-Folge

Aufgabe 1

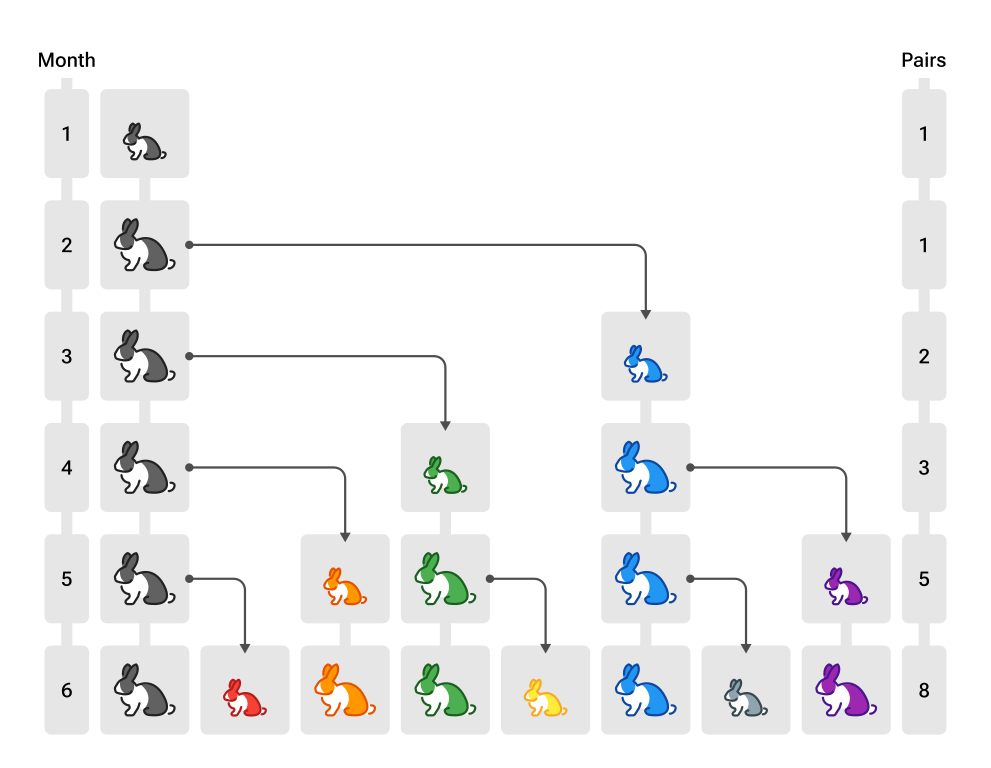
Der Rechenmeister Fibonacci - der um 1200 in Pisa lebte - hat sich mit einer Folge beschäftigt, die man mit einer Kaninchenvermehrung verdeutlichen kann:

Wir betrachten die Folge, die die Anzahl der Kaninchenpaare beschreibt.

$a_n$: Anzahl der Kaninchenpaare zu Beginn des $n$-ten Monats (für $n = 1; 2; 3; ...$)

(a) Führe die Zahlenfolge $a_1; a_2; a_3; ...$ mindestens um 3 Schritte weiter.

$\left( a_n \right)$: $1; 1; 2; 3; 5; 8; ...$

(b) Erläutere die Berechnungslogik, die man benutzen kann, um das nächste Folgenglied zu berechnen.

(c) Ergänze die rekursive Berechnungsformel für die Folge $\left( a_n \right)$.

$a_1 = 1$
$a_2 = 1$
$a_{n+2} = ...$ (für $n = 1; 2; 3; ...$)

Mehr zur Fibonacci-Folge

In der Aufgabe hast du eine rekursive Darstellung der Fibonacci-Folge erarbeitet. Doch es gibt noch viel mehr zu dieser Folge zu sagen:

So könnte man sich fragen, ob es eigentlich auch eine explizite Formel gibt. Tatsächlich gibt es die – sie ist aber recht kompliziert: Insbesondere kommen in der expliziten Formel mehrere irrationale Zahlen (Zahlen, die man nicht als Bruch darstellen kann) vor und trotzdem sind die Folgenglieder jeweils natürliche Zahlen.

Auch das Verhältnis zweier benachbarter Fibonacci-Zahlen ist interessant: Es nähert sich nämlich ebenfalls einer irrationalen Zahl an – dem sogenannten Goldenen Schnitt. Dieses Verhältnis findet sich auch an verschiedenen Stellen in der Natur (von Blättern über Kristalle bis zu schwarzen Löchern) und in der Kunst und Fotografie.

Dass der goldene Schnitt in der Natur vorkommt, geht mindestens in manchen Fällen darauf zurück, dass die Fibonacci-Folge ebenfalls in der Natur präsent ist. Mehr dazu erfährst du in diesem Video von Professor Albrecht Beutelspacher in der BR-Mediathek.