Strukturierung – 3D-Koordinatensysteme
Vereinbarungen
Auf der letzten Seite haben wir gesehen, dass es viele mathematisch richtige und sinnvolle Möglichkeiten gibt, wie man 3D-Koordinatensysteme zeichnen kann. Dennoch werden wir uns nun auf eine Art festlegen. Eine solche Vereinbarung nennt man in der Mathematik eine Konvention.
Aufgabe 1 (Einstieg)
(a) 💬 Begründe, dass es sinnvoll ist, Konventionen für die Gestaltung des Koordinatensystems festzulegen.
(b) Finde noch mindestens drei weitere Konventionen, die du im Mathematik-Unterricht kennengelernt hast. Tipp: Auch gelernte Notationen sind Konventionen.
Ein Koordinatensysteme für 3D-Darstellungen festlegen
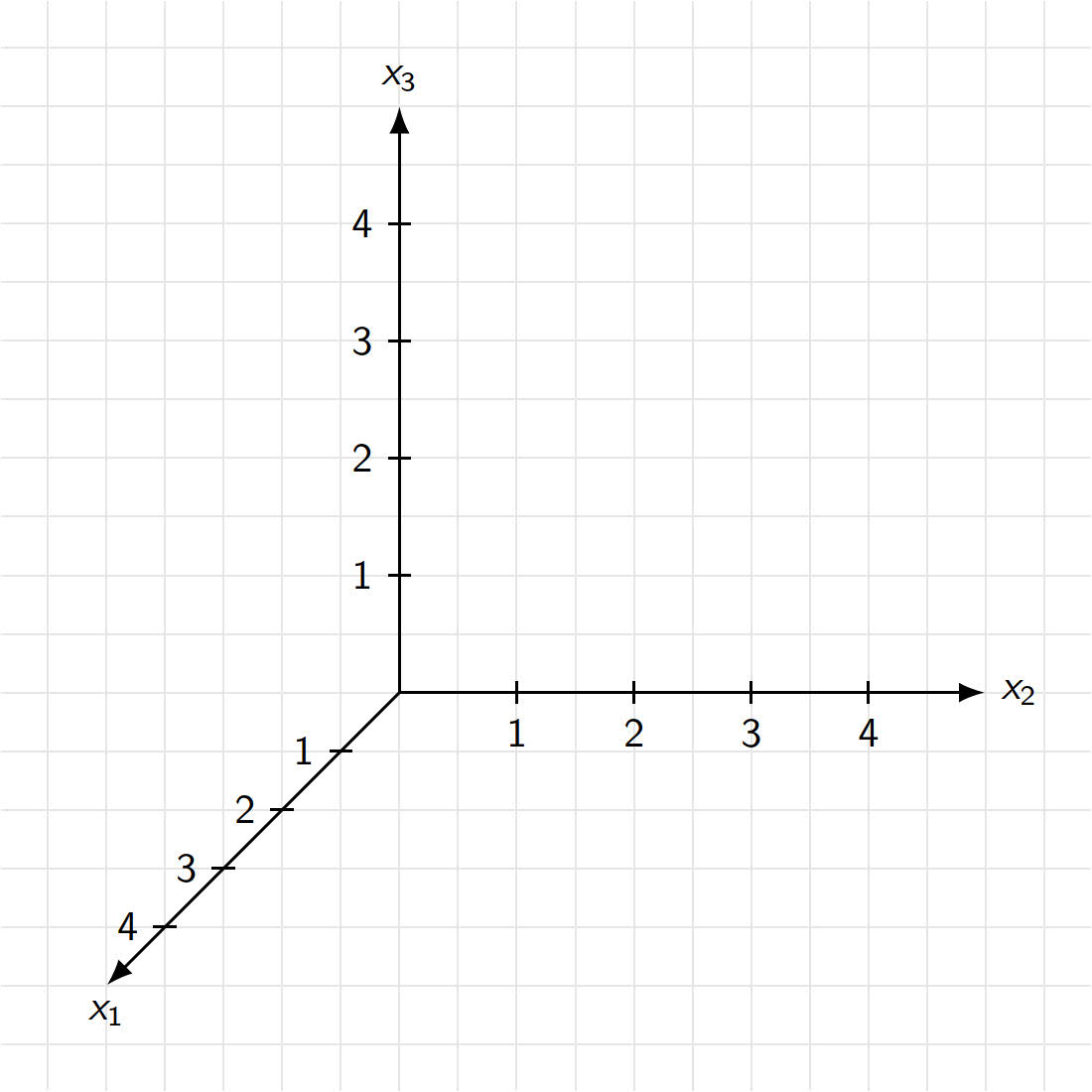
Ein 3D-Koordinatensystem benutzt man, um die Position von Punkten im Raum mit Hilfe von Zahlen zu beschreiben. Ein 3D-Koordinatensystem ist analog zu einem 2D-Koordinatensystem aufgebaut: Es besteht also aus drei Achsen (Tiefe, Breite, Höhe), die im Raum zueinander senkrecht stehen und sich im Ursprung schneiden.
Die Lage eines Punktes kann man dann mithilfe eines Zahlentripels (Liste dreier Zahlen) darstellen.
Beachte:
- Die Achsen werden üblicherweise als $x_1$-Achse, $x_2$-Achse und $x_3$-Achse bezeichnet. Man benennt sie reihum gegen den Uhrzeigersinn.
- Die $x_1$-Achse wird oft so gezeichnet, dass sie nach vorne zeigt. Da es keine dritte Dimension auf dem Papier gibt, wird sie im 45°-Winkel dargestellt.
- Damit 3D-Objekte „richtig“ aussehen, wird die $x_1$-Achse verkürzt: Eine Einheit auf den anderen Achsen (also zwei Kästchen) entsprechen auf der $x_1$-Achse einer Kästchendiagnonale.
Punkte ins 3D-Koordinatensystem einzeichnen
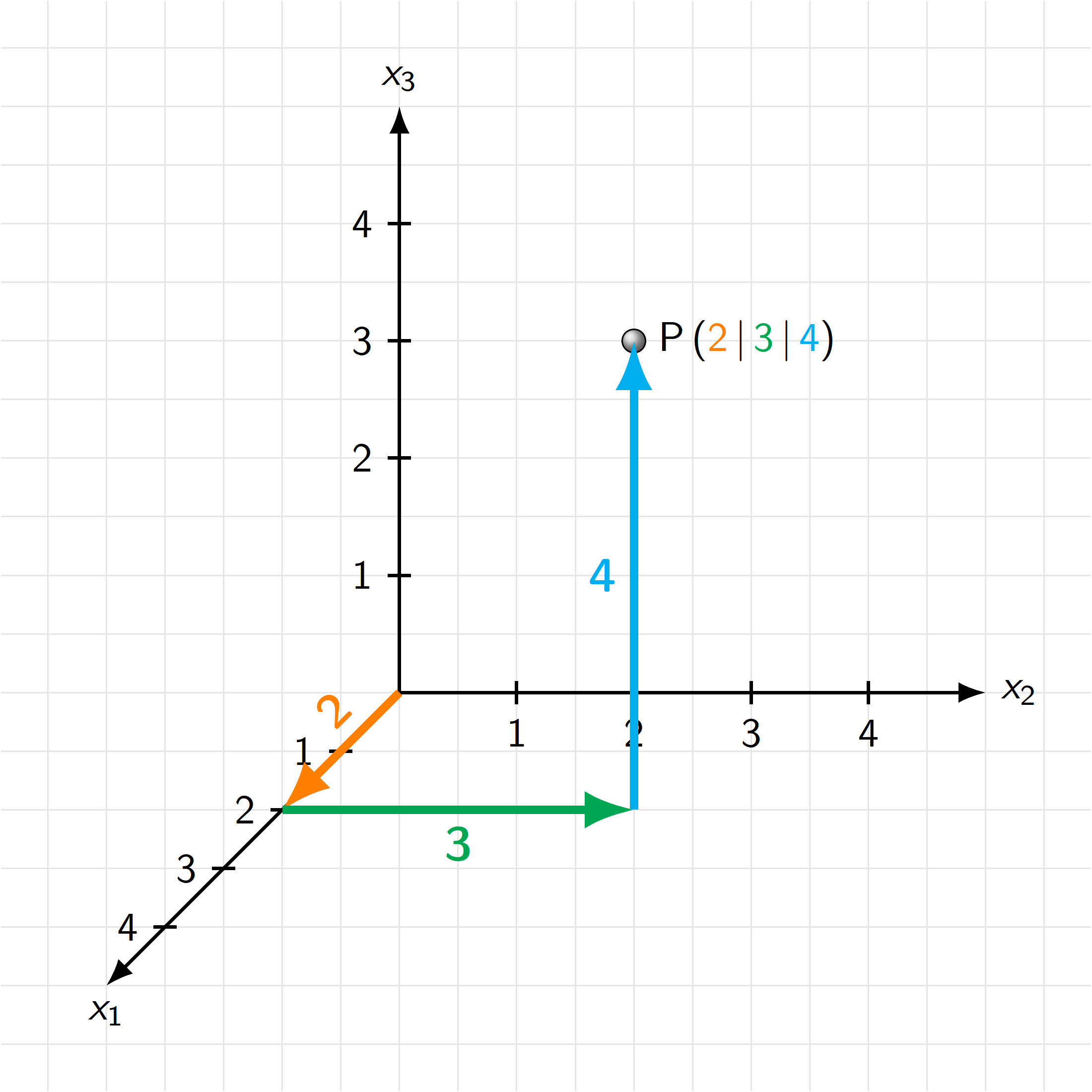
Beispiel: Die folgende Abbildung zeigt, wie man Punkte mit vorgegebenen Koordinaten in ein 3D-Koordinatensystem einzeichnet.
Aufgabe 2 (Erarbeitung und Sicherung)
(a) ✏️️ Zeichne ein 3D-Koordinatensystem auf Karopapier und zeichne dort die Punkte $A(1|2|3)$, $B(2|-1|2)$ und $C(-1|-1|-3)$ ein.
(b) ✏️️ Trage deine bisherigen Ergebnisse in der oberen Hälfte dieses Wissensspeichers ein.
Was ist ein Wissensspeicher?
Im Wissensspeicher soll übersichtlich und prägnant das neu Gelernte dokumentiert werden. Die vorgegebene Struktur auf dem Wissensspeicher soll sicherstellen, dass alles Wichtige festgehalten wird; so werden z.B. nicht nur Definitionen, sondern in der Regel auch Beispiele, Vernetzungen oder Konventionen gefordert. Der Wissensspeicher kann verwendet werden, um ein im Unterricht erstelltes Tafelbild einfacher ins Heft zu übertragen. Es ist mit ihm aber auch möglich, die Sicherung stärker schüler:innen-orientiert zu gestalten: Je nach Unterrichtsgestaltung können die Schüler:innen nach einer Erarbeitung und Besprechung den gesamten Wissensspeicher selbst ausfüllen (im Unterricht, ggf. auch in der Hausaufgabe) oder hierfür zusätzlich dieses Online-Schulbuch zu Hilfe nehmen.
Aufgabe 3 (Vertiefung)
(a) ✏️️ Zeichne auf kariertes Papier ein 3D-Koordinatensystem. Wähle dann selbst die Koordinaten eines Punktes aus und trage ihn in das Koordinatensystem ein. Notiere die Koordinaten auf der Rückseite.
(b) Lass nun eine andere Person die Koordinaten des Punktes ablesen. Diskutiert, was euch dabei auffällt.
Du kannst für die Aufgabe diese Vorlage verwenden.
Punkte im 3D-Koordinatensystem ablesen
Beobachtung
Achtung: In einem 3D-Koordinatensystem auf Papier kann man die Koordinaten eines Punktes nicht eindeutig ablesen.
Aufgabe 4 (Vertiefung und Sicherung)
(a) Erkläre diese Beobachtung noch einmal an dem Applet unter der Aufgabe.
(b) Finde eine dritte Möglichkeit für Koordinaten des eingezeichneten Punktes.
(c) ✏️️ Notiere dir die Beobachtung mit eigenen Beispielen in der unteren Hälfte des Wissensspeichers.
Zum Herunterladen: punktBestimmenMitButton.ggb
In den Übungsaufgaben wird das genauer vertieft.

