Zusammenfassung – 3D-Koordinatensysteme
Positionsbeschreibung in einem Koordinatensystem
Koordinatensysteme werden sowohl in der realen Welt als auch in der abstrahierenden Mathematik benutzt, um Positionen von Objekten präzise zu beschreiben.
3D-Koordinatensystem
Ein 3D-Koordinatensystem benutzt man, um die Position von Punkten im Raum mit Hilfe von Zahlen zu beschreiben. Wir verwenden hier folgende Konventionen:
- Das Koordinatensystem besteht aus drei Achsen, mit denen man Tiefe, Breite und Höhe zu einem Bezugspunkt beschreibt.
- Die drei Achsen sind paarweise senkrecht zueinander angeordnet und schneiden sich im Ursprung (als Bezugspunkt).
- Die Achsen werden als $x_1$-Achse, $x_2$-Achse und $x_3$-Achse bezeichnet.
- Die $x_1$-Achse zeigt
nach vorne
, die $x_2$-Achsenach rechts
und die $x_3$-Achsenach oben
.
Die Lage eines Punktes kann man dann mithilfe eines Zahlentripels (Liste dreier Zahlen) darstellen.
Zum Herunterladen: koordinatenPunkt3D.ggb
Im Applet ist ein Punkt $P$ mit den Koordinaten $P(4|3|5)$ zu sehen: Man erhält ihn vom Ursprung aus, indem man sich $4$ Einheiten in $x_1$-Richtung (rot dargestellt), $3$ Einheiten in $x_2$-Richtung (grün dargestellt) und $5$ Einheiten in $x_3$-Richtung (blau dargestellt) bewegt. Den Punkt $P(4|3|5)$ kann man auch mit dem zugehörigen Orstvektor $\vec{p} = \begin{pmatrix} 4 \\ 3 \\ 5 \end{pmatrix}$ beschreiben.
3D-Darstellungen
Das Grundproblem bei 3D-Darstellungen besteht darin, drei Dimensionen in zwei Dimensionen
einzupacken.
Ziel ist es, 3-dimensionale Objekte in einer 2-dimensionalen Ebene so darzustellen,
dass man räumliche Strukturen möglichst gut erkennen kann.
| dynamische Darstellung in einem drehbaren Koordinatensystem | statische Darstellung in einem Koordinatensystem |
|---|---|
Es gibt viele sinnvolle Möglichkeiten, wie man 3D-Koordinatensysteme zweidimensional zeichnen kann. In der Übersicht oben kann man im rechten Applet den Neigungswinkel $\alpha$ und den Verkürzungsfaktor $v$ bei Zeichnen der nach vorne zeigenden $x_1$ Achse variieren und kann so verschiedene Darstellungsmöglichkeiten einstellen. Wir verwenden hier eine an das Karopapier im Heft angelehnte Darstellung, die in der folgenden Abbildung verdeutlicht wird.
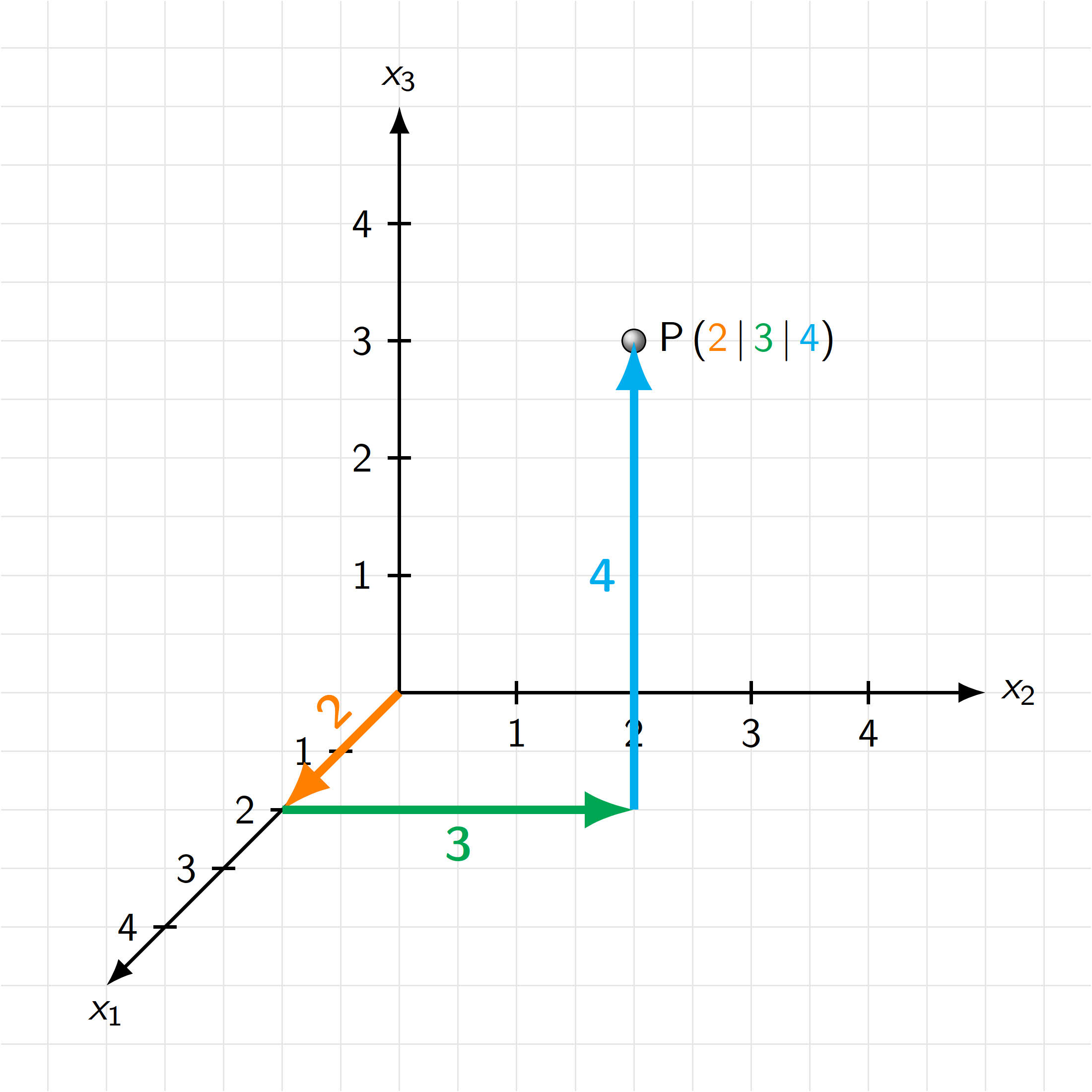
Achtung: In einem 3D-Koordinatensystem auf Papier kann man die Koordinaten eines Punktes nicht eindeutig ablesen. Das zeigt das folgende Applet.
Zum Herunterladen: punktBestimmenMitButton.ggb

