Strukturierung - Lösungsmengen von linearen Gleichungssystemen
Die mögliche Anzahl der Lösungen angeben
Hier geht es um die Frage, wie viele Lösungen ein LGS haben kann.
Aufgabe 1
Fasse die Ergebnisse aus den vorangehenden Abschnitten zusammen. Gehe im Folgenden immer davon aus, dass in einem LGS mindestens eine Variable vorkommt.
| Anzahl der Gleichungen | Anzahl der Variablen | mögliche Anzahl der Lösungen | |
|---|---|---|---|
| LGS mit | 1 | 2 | |
| LGS mit | 2 | 2 | |
| LGS mit | 1 | 3 | |
| LGS mit | 2 | 3 | |
| LGS mit | 3 | 3 |
Die Vorgehensweise beschreiben
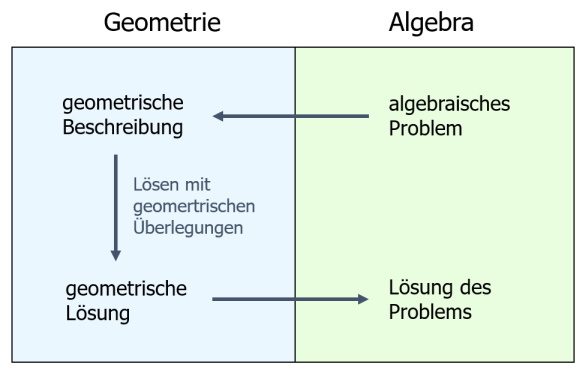
In den vorangehenden Abschnitten wurde das algebraische Problem "Wie viele Lösungen kann ein LGS haben?" mit geometrischen Überlegungen gelöst.
Aufgabe 2
Beschreibe die Vorgehensweise. Beschreibe hierzu möglichst genau, wie die folgenden Schritte im Fall linearer Gleichungssysteme mit 3 Variablen durchgeführt wurden.
Schritt 1: Das algebraische Problem in ein geometrisches Problem übersetzen
Schritt 2: Das geometrische Problem lösen
Schritt 3: Die Lösung des geometrischen Problems algebraisch deuten
Quellen
- [1]: Algebraisches Problem geometrisch lösen - Urheber: KB - Lizenz: inf-schule.de