Ergebnisse deuten
Die im Modell erzielten Ergebnisse im Kontext deuten
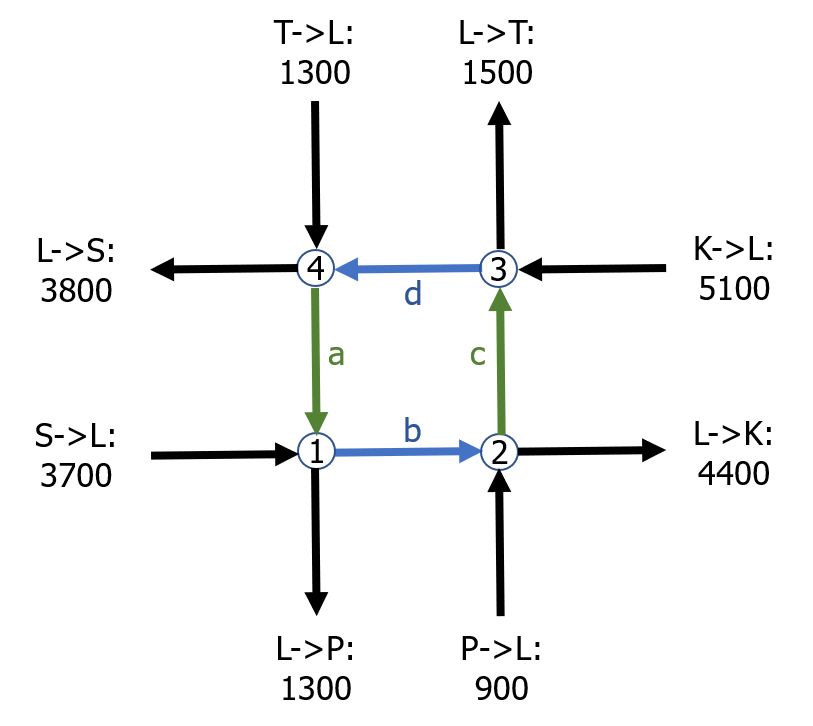
Wir sind von folgenden Modellannahmen ausgegangen.
Anschließend haben wir das zugehörige lineare Gleichungssystem gelöst.
$\begin{array}{lrcrcrcr} [1] &\quad 3700 + a & = & 1300 + b \\ [2] &\quad 900 + b & = & 4400 + c \\ [3] &\quad 5100 + c & = & 1500 + d \\ [4] &\quad 1300 + d & = & 3800 + a \end{array}$
Das LGS hat unendlich viele Lösungen. Wir können die Lösungen mit einer beliebigen reellen Zahl $t$ so beschreiben:
- $a = t + 1100$
- $b = t + 3500$
- $c = t$
- $d = t + 3600$
Aufgabe 1
Kann man tatsächlich jede reelle Zahl als sinnvolle Lösung im Kontext ansehen? Beurteile z.B. die Wahl $t = -100$. Begründe, dass $t$ folgende Bedingung erfüllen muss:
$t \geq 0$
Aufgabe 2
(a) Begründe, warum $t = 1000000$ nicht möglich ist.
(b) Begründe, dass die folgende Bedingung immer erfüllt sein muss:
$a + b + c + d \leq 11000$
Was würde es in der Realität bedeuten, wenn $a + b + c + d = 11000$ gelten würde? erläutere kurz.
(c) Setze die oben aufgeführten Ergebnisse für $a$, $b$, $c$, $d$ in die Ungleichung $a + b + c + d \leq 11000$ ein und folgere hieraus, dass auch diese Bedingung für $t$ gelten muss:
$t \leq 700$
Aufgabe 3
Mit welchem maximalen LKW-Verkehrsaufkommen muss man am Autobahnkreuz Landstuhl-West in den Abschnitten $a$, $b$, $c$ und $d$ rechnen, wenn man die oben angegebenen (gerundeten) Messwerte zu Grunde legt? Bestimme abschließend diese Werte.
Quellen
- [1]: Modell zur Verkehrsdichte am AK Landstuhl-West - Urheber: KB - Lizenz: inf-schule.de