Eine Modellierung
Die Problemsituation mathematisch modellieren
Wir betrachten folgende Problemsituation.
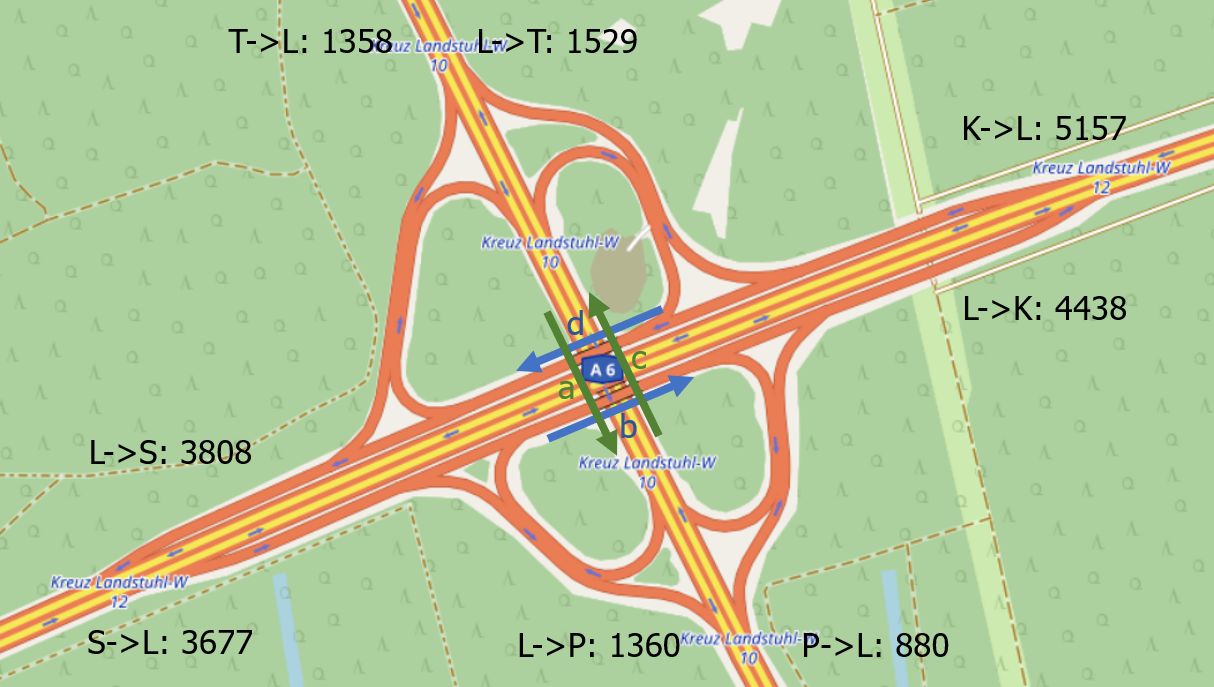
Gegeben sind die Werte für die durchschnittliche Anzahl der Schwerverkehrsteilnehmer, die pro Stunde auf das Autobahnkreuz zu bzw. vom Autobahnkreuz wegfahren: $T->L=1358$, $L->T=1529$, usw..
Gesucht sind die Werte für die durchschnittliche Anzahl der Schwerverkehrsteilnehmer, die pro Stunde die Autobahnbrücke über- bzw. unterqueren. Diese Werte werden mit $a$, $b$, $c$, $d$ bezeichnet.
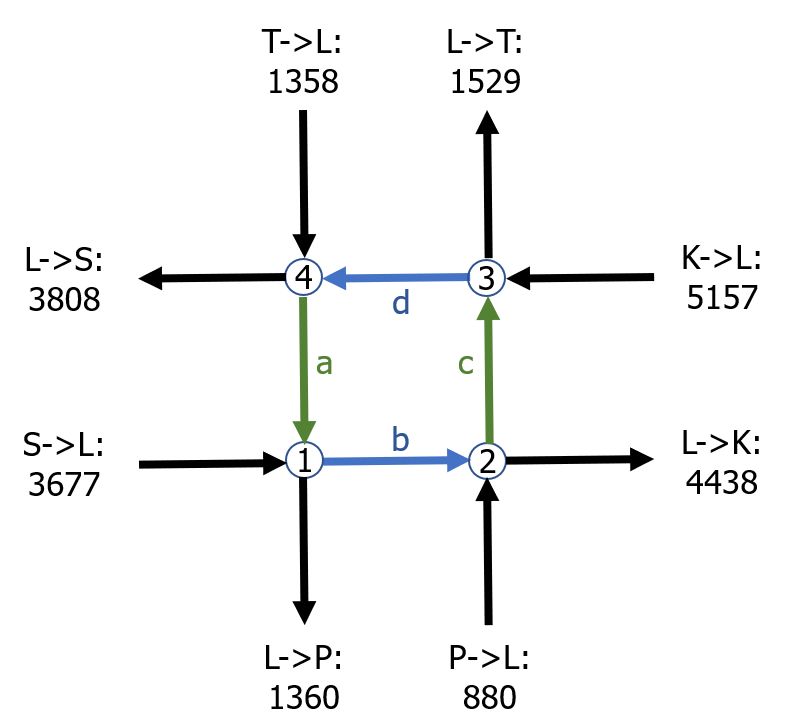
Beim mathematischen Modellieren fokussiert man sich auf die Daten, die für die Problembearbeitung relevant sind und lässt alles andere weg. Im vorliegenden Problemkontext könnte eine vereinfachte Darstellung der Problemsituation so aussehen.
Aufgabe 1
Erläutere die Darstellung. Erkläre z.B. wie ein LKW im realen Autobahnkreuz bzw. im vereinfachten Modell von Saarbrücken nach Trier fährt.
Ein- und Ausfahr-Bilanzen erstellen
Zwischen den verschiedenen Verkehrsangaben gibt es Zusammenhänge. Diese lassen sich mit Hilfe von Gleichungen beschreiben.
$\begin{array}{lrcrcrcr} [1] &\quad 3677 + a & = & 1360 + b \\ [2] &\quad ... \\ [3] &\quad ... \\ [4] &\quad ... \end{array}$
Aufgabe 2
(a) Deute die Gleichung $[1]$, z.B. so: Alle LKWs, die von $S$ oder vom Abschnitt $a$ aus kommen, ...
(b) Stelle entsprechende Gleichungen für die anderen Knotenpunkte auf.
Quellen
-
[1]: Verkehrsdichte Brücke - Urheber: KB - Lizenz: inf-schule.de
unter Verwendung von:
- - Urheber: OpenStreetMap - Lizenz: Open Data Commons Open Database License 1.0
- [2]: Modell zur Verkehrsdichte am AK Landstuhl-West - Urheber: KB - Lizenz: inf-schule.de