o-mathe | Wie berechnet man Nullstellen? » Berechnung durch Auflösen der Gleichung

Berechnung durch Auflösen der Gleichung

Wir betrachten den Fall, dass die Nullstellen einer linearen Funktion gesucht sind.

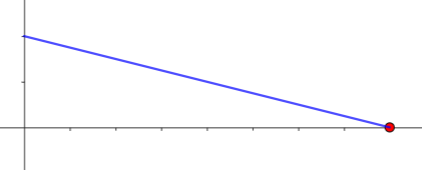
geg.: $f (x) = 2 - \frac{1}{4} x$

ges.: Nullstellen von $f$

Ansatz: $f (x) = 0$

Aufösen der Gleichung nach $x$ mit Hilfe von Äquivalenzumformungen:

$\begin{array}{lcl} 2 - \frac{1}{4} x & = & 0 \\ 2 & = & \frac{1}{4} x \\ 8 & = & x \end{array}$

Ergebnis: Die gesuchte Nullstelle ist $x = 8$ .

Bestimme analog die Nullstellen der folgenden Funktionen.

☑ Lösungscheck

Die unsortierten Lösungen sind –4; –1; 5; 6.