Einstieg
Das Problem klären
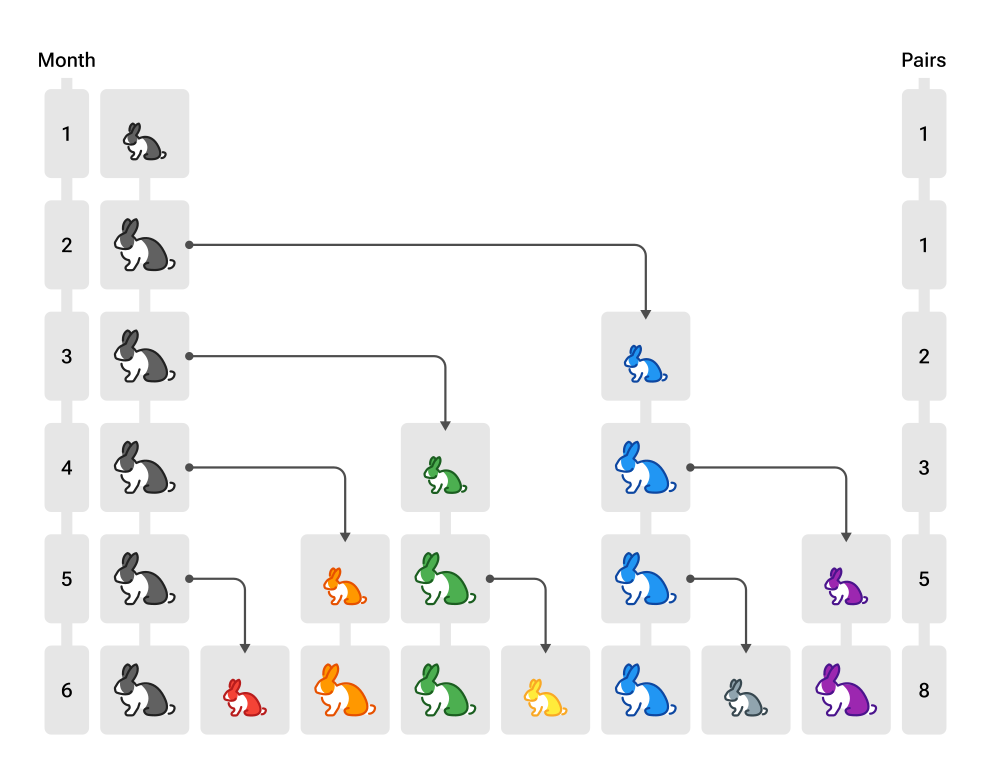
Der Rechenmeister Fibonacci - der um 1200 in Pisa lebte - hat sich mit einer Folge beschäftigt, die man mit einer Kaninchenvermehrung verdeutlichen kann:
Kaninchenvermehrung
- Zu Beginn gibt es $1$ Kaninchenpaar.
- Vom zweiten Lebensmonat an beginnt ein Kaninchenpaar sich fortzupflanzen.
- Jedes Kaninchenpaar erzeugt ein weiteres Paar pro Monat.
Wir betrachten die Folge, die die Anzahl der Kaninchenpaare beschreibt.
$a_n$: Anzahl der Kaninchenpaare zu Beginn des $n$-ten Monats (für $n = 1; 2; 3; ...$)
Diese Folge wird auch Fibonacci-Folge genannt.
Aufgabe 1
(a) Führe die Zahlenfolge $a_1; a_2; a_3; ...$ mindestens um 3 Schritte weiter.
$\left( a_n \right)$: $1; 1; 2; 3; 5; 8; ...$
(b) Erläutere die Berechnungslogik, die man benutzen kann, um das nächste Folgenglied zu berechnen.
(c) Ergänze die rekursive Berechnungsformel für die Folge $\left( a_n \right)$.
$a_1 = 1$
$a_2 = 1$
$a_{n+2} = ...$ (für $n = 1; 2; 3; ...$)
(d) Warum ist es sehr aufwendig, einen Wert wie z.B. $a_{1000}$ zu berechnen?
Zielsetzung
Die Folgenglieder der Fibonacci-Folge lassen sich mit einer naheliegenden rekursiven Darstellung der Folge berechnen. Interessant wäre es, wenn man für die Fibonacci-Folge auch eine explizite Darstellung angeben könnte. Tatsächlich gibt es eine solche Darstellung. Die ist aber recht kompliziert und gar nicht so leicht zu finden. Ziel ist es hier, diese Darstellung zu entwickeln. Wir verwenden dabei einen Ansatz, bei dem Eigenvektoren eine zentrale Rolle spielen.
Quellen
- [1]: Kaninchenvermehrung - Urheber: Romain - Lizenz: Creative Commons BY-SA 4.0