Zusammenfassung - Ableitungsfunktion
Die Grundidee
Die Ableitung $f'(x)$ beschreibt die lokale Änderungsrate der Ausgangsfunktion $f$ an der Stelle $x$. Geometrisch lässt sich diese Ableitung $f'(x)$ als Steigung von Graph $f$ im Punkt $P(x|f(x))$ deuten.
Wenn man die Zuordnung $x \rightarrow f'(x)$ in den Blick nimmt, erhält man eine neue Funktion - die Ableitungsfunktion $f'$ zur Ausgangsfunktion $f$.
Zum Herunterladen: ableitungsfunktion1.ggb
Im vorliegenden Beispiel ordnet die Ableitungsfunktion $f'$ dem $x$-Wert $2$ die Zahl $f'(2) = 0$ zu - also genau die Steigung von Graph $f$ im Punkt $P(2|...)$. Die Gesamtheit all dieser Zuordnungen liefert einen neuen Graph, den man in einem (eigenen) Koordinatensystem veranschaulichen kann.
Eine mathematische Präzisierung
Die Ableitungsfunktion lässt sich somit wie folgt mathematisch beschreiben.
Die Ableitungsfunktion $f'$ zu einer Ausgangsfunktion $f$ ordnet jedem $x$-Wert die Ableitung von $f$ an dieser Stelle zu - sofern diese Ableitung existiert.
Der Begriff „Ableiten“ wird benutzt, um den Vorgang zu beschreiben, die Ableitungsfunktion zu einer Ausgangsfunktion zu ermitteln. Statt „Ableiten“ benutzt man synonym auch den Begriff „Differenzieren“.
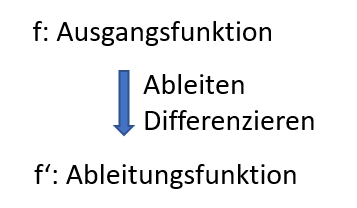
Wir sind beim Ableiten bisher grafisch vorgegangen. Wir haben aus dem Graphen der Ausgangsfunktion (näherungsweise) den Graph der Ableitungsfunktion konstruiert. Diesen Vorgang nennt man auch „grafisch Ableiten“ oder „grafisch Differenzieren“. In den folgenden Unterkapiteln werden wir Verfahren entwickeln, wie man rechnerisch (man sagt auch „algebraisch“) die Ableitungsfunktion zu einer Ausgangsfunktion bestimmen kann.
