Integral und Flächeninhalte
Orientierte Flächeninhalte betrachten
Im Kapitel "Rekonstruktion eines Bestandes" hast du gesehen, dass man den Bestand aus einer Änderungsratenfunktion erhält, indem man orientierte Flächeninhalte bestimmt.
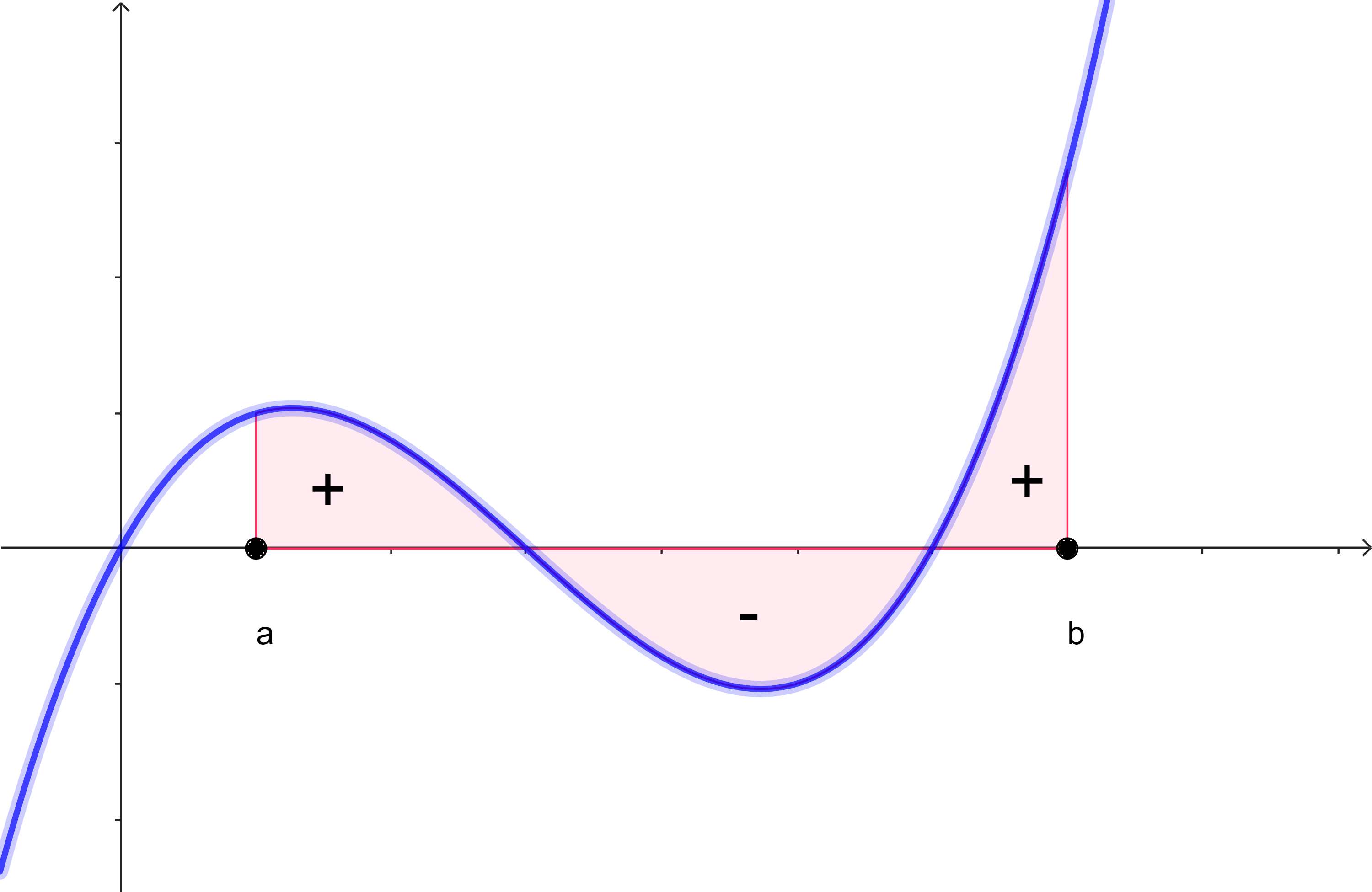
Den orientierten Flächeninhalt einer Funktion $f$ im Intervall $a \leq x \leq b$ (in dem die Funktion definiert ist) erhält man, indem man die Flächeninhalte der Flächenstücke zwischen Graph $f$ und der $x$-Achse von $a$ bis $b$ in "orientierter Form" aufsummiert. Die Flächeninhalte von Flächenstücken oberhalb der $x$-Achse werden dabei positiv, die Flächeninhalte von Flächenstücken unterhalb der $x$-Achse negativ gewertet.
Den Zusammenhang zum Integral herstellen
Den orientierten Flächeninhalt kann man mit dem Integral bestimmen. Hier sind noch einmal die Grundideen zusammengestellt.
Zum Herunterladen: orientierteflaecheninhalte2.ggb
Wir betrachten folgende Situation: Gegeben ist eine Funktion $f$ und ein Intervall $a \leq x \leq b$, das in der Definitionsmenge der Funktion $f$ liegt.
- In dem Intervall $a \leq x \leq b$ wird die Funktion $f$ mit Treppenfunktionen angenähert. Hierzu wird das Intervall $a \leq x \leq b$ in $n$ Teile zerlegt.
- Die untere Treppenfunktion ist so festgelegt, dass die "Treppenhöhe" jeweils dem kleinsten Funktionswert von $f$ im betreffenden Teilintervall entspricht. Die obere Treppenfunktion ist so festgelegt, dass die "Treppenhöhe" jeweils dem größten Funktionswert von $f$ im betreffenden Teilintervall entspricht.
- Zu den beiden Treppenfunktion werden Produktsummen gebildet. Hierzu werden alle zum Intervall gehörenden Terme der Gestalt "Stufenhöhe mal Stufenbreite" aufaddiert. Beachte, dass die Stufenhöhe hier auch eine negative Zahl sein kann. Diese Produktsummen liefern die orientierten Flächeninhalte zu den entsprechenden Treppenfiguren (die man aus den Treppenfunktion erhält).
- Die Produktsumme zur unteren Treppenfigur liefert die Untersumme $U_n$, die Produktsumme zur oberen Treppenfigur die Obersumme $O_n$.
- Wenn man die Anzahl $n$ der Unterteilungen gegen Unendlich gehen lässt, dann wird die Annäherung der Ausgangsfunktion $f$ durch die Treppenfunktionen immer besser. Ebenso nähern die Treppenfiguren zu den Treppenfunktion die Flächenstücke zwischen Graph $f$ und der $x$-Achse immer besser an. Der Grenzwert von Unter- und Obersummen liefert somit den orientierten Flächeninhalt von $f$ im Intervall $a \leq x \leq b$.
- Den Grenzwert von Unter- und Obersummen bezeichnet man auch als Integral von $f$ von $a$ bis $b$.
- Man nutzt die Schreibweise $I_a(b) = \int\limits_{a}^{b} f(x) dx$ für das Integral von $f$ von $a$ bis $b$.
Integrale lassen sich also als orientierte Flächeninhalte deuten:
Wenn die Funktion $f$ im Intervall $a \leq x \leq b$ definiert ist, dann entspricht das Integral $I_a(b) = \int\limits_{a}^{b} f(x) dx$ geometrisch dem orientierten Flächeninhalt zwischen Graph $f$ und der $x$-Achse von $a$ bis $b$.

