Erarbeitung
Zur Orientierung
Ziel ist es hier, die Entwicklung einer Mäusepopulationen zu modellieren und im Modell zu simulieren.
Ein Populationsentwicklungsmodell entwickeln
Wir gehen hier von stark vereinfachten Rahmenbedingungen aus.
Entwicklung einer Mäusepopulation
- Wir betrachten ausschließlich weibliche Mäuse, da nur sie neue Mäuse gebären können.
- Die Mäusepopulation wird in $3$ Altergruppen aufgeteilt: junge Mäuse (im Alter von $0$ - $1$ Jahr), erwachsene Mäuse (im Alter von $1$ - $2$ Jahre) und alte Mäuse (im Alter von $2$ - $3$ Jahre).
- Wir betrachten eine schrittweise Entwicklung der Mäusepopulation. Die Schrittweite beträgt dabei $1$ Jahr.
- Die Überlebensrate junger Mäuse ist durch Restriktionen gering: Nur $10 \%$ der jungen Mäuse überleben das erste Jahr.
- Die Überlebensrate erwachsener Mäuse ist deutlich höher. $50 \%$ der erwachsenen Mäuse erreichen ein Alter von $2$ - $3$ Jahre und wechseln so in einem einem Simulationsschritt in die Klasse der alten Mäuse.
- In unserem vereinfachten Modell wird keine Maus älter als $3$ Jahre. Alle bereits alte Mäuse überleben das nächste Jahr nicht mehr.
- Junge Mäuse tragen noch wenig zur Fortpflanzung bei. Durch die starken Restriktionen erzeugt jede junge Maus pro Jahr im Mittel nur $0.5$ neue Mäuse.
- Jede erwachsene Maus erzeugt im Mittel pro Jahr wieder $4$ junge Mäuse.
- Die Fertibilität lässt mit zunehmendem Alter ab. Jede alte Maus erzeugt im Mittel pro Jahr nur noch $2$ junge Mäuse.
Beachte: Die hier betrachteten Überlebensraten und Vermehrungsraten sind fiktive Werte für eine Population mit starken Restriktionen. In der Realität sind bei guten Bedingungen die Vermehrungsraten deutlich höher.
Aufgabe 1
Ergänze den folgenden Übergangsgraph zur Beschreibung der Entwicklung der Mäusepopulationsen. Ergänze an den rot dargestellten Übergängen die Überlebensraten und an den blau dargestellten Übergängen die Vermehrungsraten.
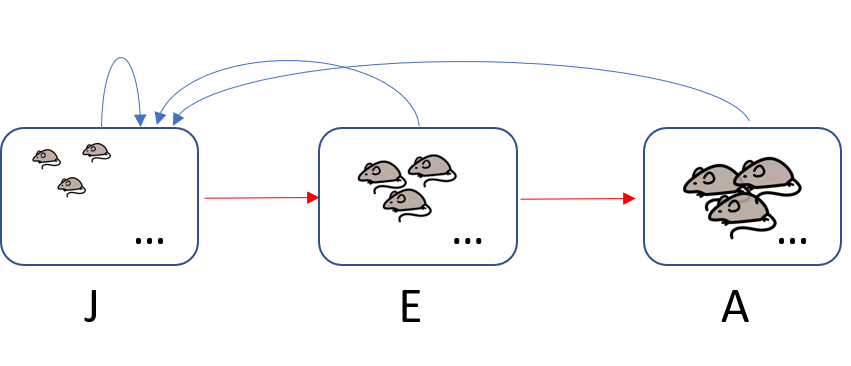
Aufgabe 2
Die Ausgangspopulation soll aus $100$ jungen Mäusen, $100$ erwachsenen Mäusen sowie $100$ alten Mäusen bestehen. Berechne die Populationswerte nach $1$ und nach $2$ Schritten (bzw. Jahren). Die Tabelle enthält Eingabefelder, die dir nach der Eingabe eine Rückmeldung geben, ob du die Populationswerte richtig bestimmt hast.
| Schritte | A | B | C |
|---|---|---|---|
| $0$ | $100$ | $100$ | $100$ |
| $1$ | |||
| $2$ |
Aufgabe 3
Verwende das Simulationstool ProSiTo zur Modellierung und zur Simulation der Populationsentwicklung.
(a) Erzeuge zunächst die Zustände (das sind hier die Altersklassen).
(b) Erzeuge anschließend die Zustandsübergänge und gib die zugerörigen Übergangsraten ein.
(c) Gib die Ausgangspopulation ein: $100$ junge Mäuse, $100$ erwachsene Mäuse sowie $100$ alte Mäuse. Führe mit ProSiTo die Simulation der Populationsentwicklung über mehrere Schritte durch. Kontrolliere, ob du die in Aufgabe 2 selbst berechneten Werte erhältst. Beobachte, auch, wie sich die Population auf lange Sicht entwickelt. Was fällt auf?
Aufgabe 2
Variiere die Ausgangsverteilung der jungen, erwachsenen und alten Mäuse. Beschreibe, wie sich die Population langfristig entwickelt.

