Übungen - Vertrauensintervalle für Wahrscheinlichkeiten

Aufgabe 1

Ein Pyramidenwürfel wird 120-mal geworfen.

Zum Herunterladen: wuerfelnPWVersuchsreihe2.ggb

(a) Die in der Tabelle angegebenen relativen Häufigkeiten können als Schätzwerte für die Wahrscheinlichkeiten der Augenzahlen beim Pyramidenwürfel verwendt werden. Erläutere, warum diese Vorgehensweise mit viel statistischer Unsicherheit verbunden ist.

(b) Beim regelmäßigen Pyramidenwürfel wird davon ausgegangen, dass die Wahrscheinlichkeiten der „Seitenaugenzahlen“ $2$, $3$, $4$ und $5$ alle gleich sind. Überprüfe mit einem $95\%$-Sicherheitsniveau, ob die Ergebnisse in der oben gezeigten Versuchsreihe mit der Wahrscheinlichkeit $p = 0.15$ für alle „Seitenaugenzahlen“ verträglich sind.

Zum Herunterladen: prognoseintervalle1.ggb

(c) Bestimme mit dem folgenden Applet $95\%$-Vertrauensintervalle für alle Augenzahlen des Pyramidenwürfels.

Zum Herunterladen: vertrauensintervalle1.ggb

(d) Erzeuge mit einem [Neustart] eine weitere Versuchsreihe und bestimme auch für diese Reihe $95\%$-Vertrauensintervalle für alle Augenzahlen des Pyramidenwürfels. Erläutere kurz: Vertrauensintervalle hängen von den Ergebnissen einer konkret durchgeführten Versuchreihe ab.

Aufgabe 2

In einer Studie zum Substanzkonsum bei Jugendlichen und jungen Erwachsenen wurden Telefoninterviews mit Jugendlichen und jungen Erwachsenen geführt, in denen es u.a. auch um deren Alkoholkonsum ging. Gefragt wurde, ob sie regelmäßig (d.h. wöchentlich) alkoholische Getränke konsumieren. Hier die Daten der Studie:

Merkmal	Anzahl	regelmäßiger Alkoholkonsum	Vertrauensintervall
Gesamtanzahl	$2360$	$205$	$\dots \leq p \leq \dots$
männlich	$1182$	$125$
weiblich	$1178$	$78$
divers	$0$	$0$
12-13 Jahre	$1022$	$7$
14-15 Jahre	$652$	$39$
16-17 Jahre	$686$	$131$
Gymnasium	$1544$	$145$
Sonstige Schulen	$816$	$67$

Für eine Veröffentlichung sollen aus der Stichprobe Aussagen über die Gesamtheit aller Jugendlichen in Deutschland getroffen werden. Hierfür sollen $95\%$-Vertrauensintervalle für die jeweiligen Anteile (bzw. Wahrscheinlichkeiten) angegeben werden.

Bestimme diese Vertrauensintervalle. Formuliere auch eine Art Fazit der Studie, in dem auf die Vertrauensintervalle Bezug genommen wird.

Zum Herunterladen: vertrauensintervalle2.ggb

Aufgabe 3

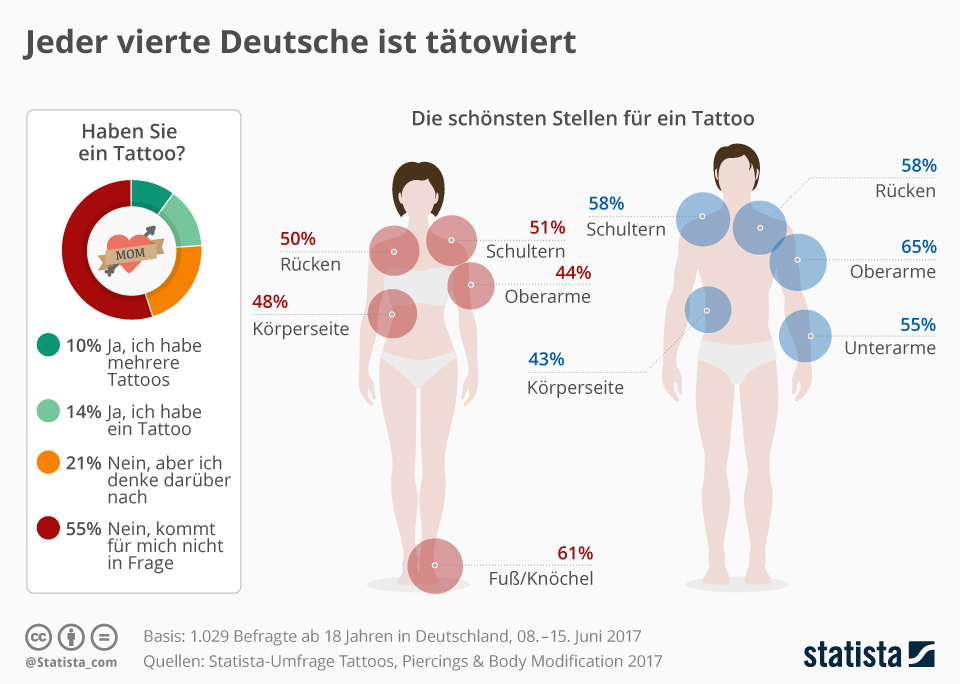
Die Grafik ist mit der Überschrift „Jeder vierte Deutsche ist tätowiert“ versehen. Zu diesem Ergebnis ist eine Befragung 2017 unter $1029$ Personen ab 18 Jahre gekommen.

(a) Schätze zunächst mit Hilfe der Angaben in der Abbildung ab, wie viele Personen eine der vier zur Verfügung gestellten Antwortalternativen gewählt haben.

(b) Bestimme Vertrauensintervalle für die jeweiligen Anteile in der Gesamtbevölkerung. Benutze hierfür eine $95\%$-Sicherheitswahrscheinlichkeit.

(c) Mache einen Vorschlag, wie die Überschrift etwas vorsichtiger gestaltet werden sollte.

Für die Berechnungen kannst du das Applet aus Aufgabe 2 verwenden.

Aufgabe 4

Zur Abschätzung, welche unmittelbaren Auswirkungen aktuelle politische Ereignisse auf das Ansehen der politischen Parteien haben, stellen Meinungsforscher die sogenannte Sonntagsfrage: „Wenn am nächsten Sonntag Wahl wäre, welcher Partei würden Sie Ihre Stimme geben?“ In der letzten Umfrage wurden $900$ Personen befragt. Dabei gaben $421$ Personen an, die neu gegründete MPD (Mathematische Partei Deutschlands) wählen zu wollen.

(a) Die Parteivorsitzenden der MPD behaupten: „Wir können noch die absolute Mehrheit holen und alleine regieren! Das ist nicht unwahrscheinlich.“ Überprüfen Sie diesen Anspruch auf einem Vertrauensniveau von $95\%$.

(b) Das Meinungsforschungsinstitut FORZA hat für die gesuchten Wahrscheinlichkeiten die Werte $45\%$ und $51\%$ berechnet. Dieses Ergebnis ist offensichtlich falsch. Erläutere, woran dies bereits zu erkennen ist, ohne überhaupt eine Rechnung durchgeführt zu haben.