Überprüfung – Berechnung von Integralen
Aufgabe 1: Richtige Lösungen finden – Teil 1
Die Abbildung zeigt ein Flächenstück, das vom Graphen der Funktion $f$ und der $x$-Achse umrandet wird.
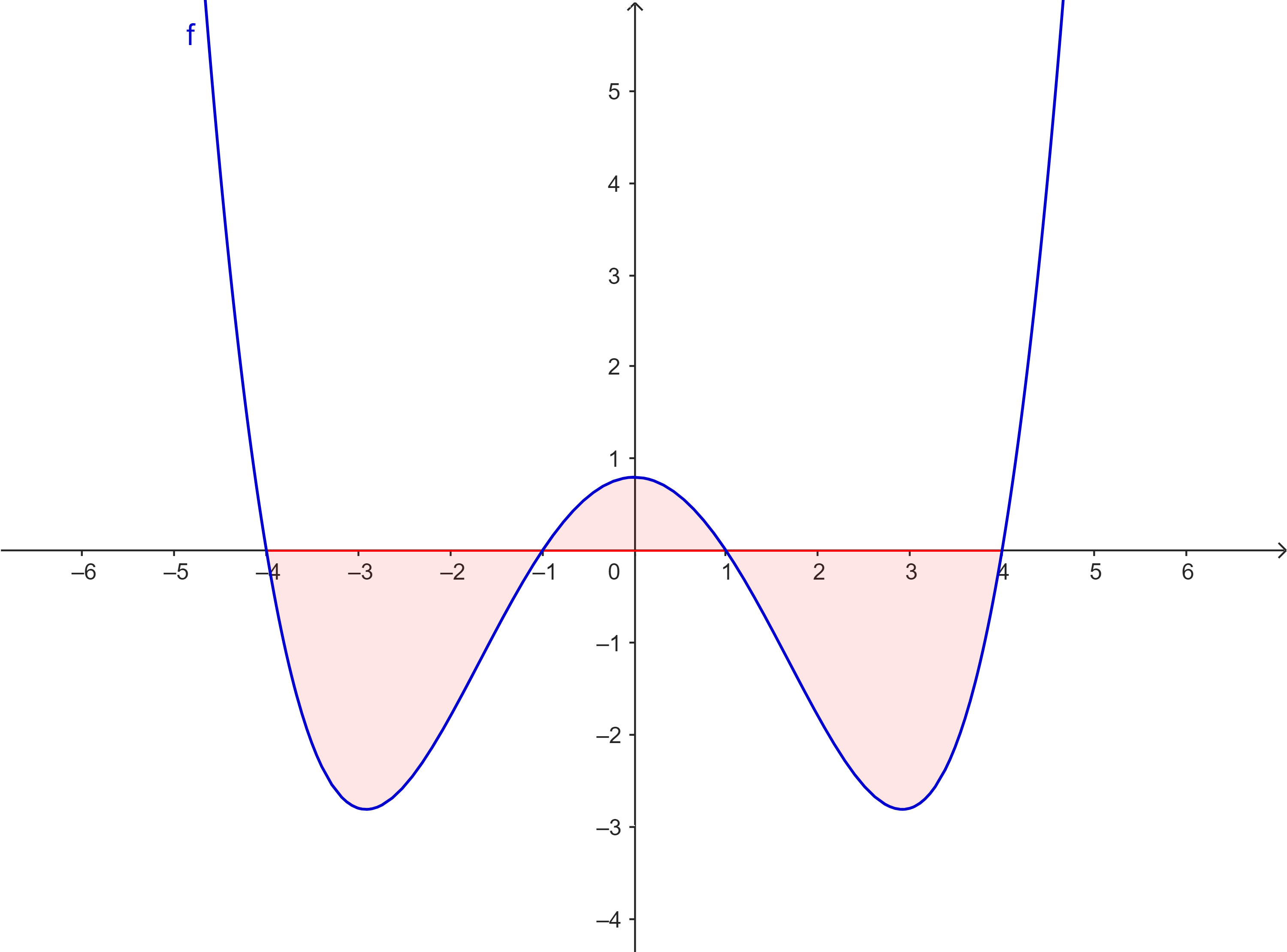
Welche der folgenden Formeln zur Berechnung des Flächeninhalts sind korrekt? Begründe jeweils.
(a) $A = \int\limits_{-4}^{4} f(x) dx$
(b) $A = | \int\limits_{-4}^{4} f(x) dx |$
(c) $A = \int\limits_{-4}^{-1} f(x) dx + \int\limits_{-1}^{1} f(x) dx + \int\limits_{1}^{4} f(x) dx $
(d) $A = -\int\limits_{-4}^{-1} f(x) dx + \int\limits_{-1}^{1} f(x) dx - \int\limits_{1}^{4} f(x) dx $
(e) $A = | \int\limits_{-4}^{-1} f(x) dx | + | \int\limits_{-1}^{1} f(x) dx | + | \int\limits_{1}^{4} f(x) dx |$
(f) $A = \int\limits_{-4}^{4} |f(x)| dx $
Aufgabe 2: Richtige Lösungen finden – Teil 2
Die Abbildung zeigt ein Flächenstück, das vom Graphen der Funktion $f$ und der Funktion $g$ umrandet wird.
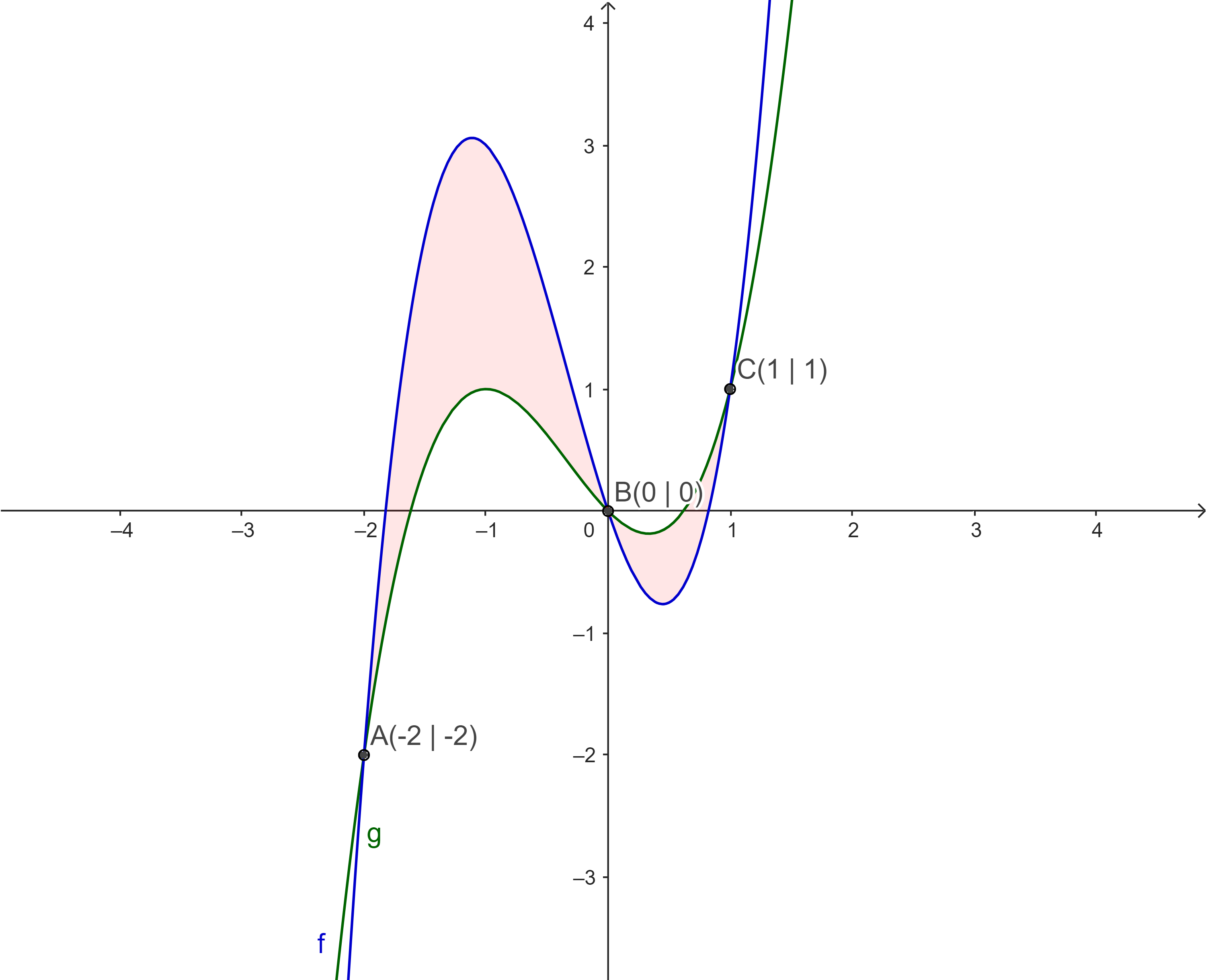
Welche der folgenden Formeln zur Berechnung des Flächeninhalts sind korrekt? Begründe jeweils.
(a) $A = \int\limits_{-2}^{1} f(x) dx - \int\limits_{-2}^{1} g(x) dx$
(b) $A = \int\limits_{-2}^{1} (f(x) - g(x)) dx$
(c) $A = \int\limits_{-2}^{1} |f(x) - g(x)| dx$
(d) $A = \int\limits_{-2}^{0} (f(x) - g(x)) dx + \int\limits_{0}^{1} (g(x) - f(x)) dx $
(e) $A = |\int\limits_{-2}^{1} (f(x) - g(x))| dx$
(f) $A = \int\limits_{-2}^{0} f(x) dx - \int\limits_{-2}^{0} g(x) dx + \int\limits_{0}^{1} g(x) dx - \int\limits_{0}^{1} f(x) dx$

