Übungen – Berechnung von Integralen
Aufgabe 1: Flächenstücke berechnen
In der Tabelle werden in der Spalte "Veranschaulichung" verschiedene Flächenstücke gezeigt, die (teilweise) von Funktionsgraphen umrandet werden.
Berechne jeweils den Flächeninhalt der Flächenstücke.
Unten findest du ein Gleichungstool, mit dem du ggf. Gleichungen lösen kannst. Damit kannst du z.B. Nullstellen oder Schnittstellen bestimmen.
Außerdem findest du einen Integralrechner, mit dem du deine Integralberechnungen kontrollieren kannst.
| Daten | Veranschaulichung | |
|---|---|---|
| (a) | $f(x) = x^2 - 4$ |
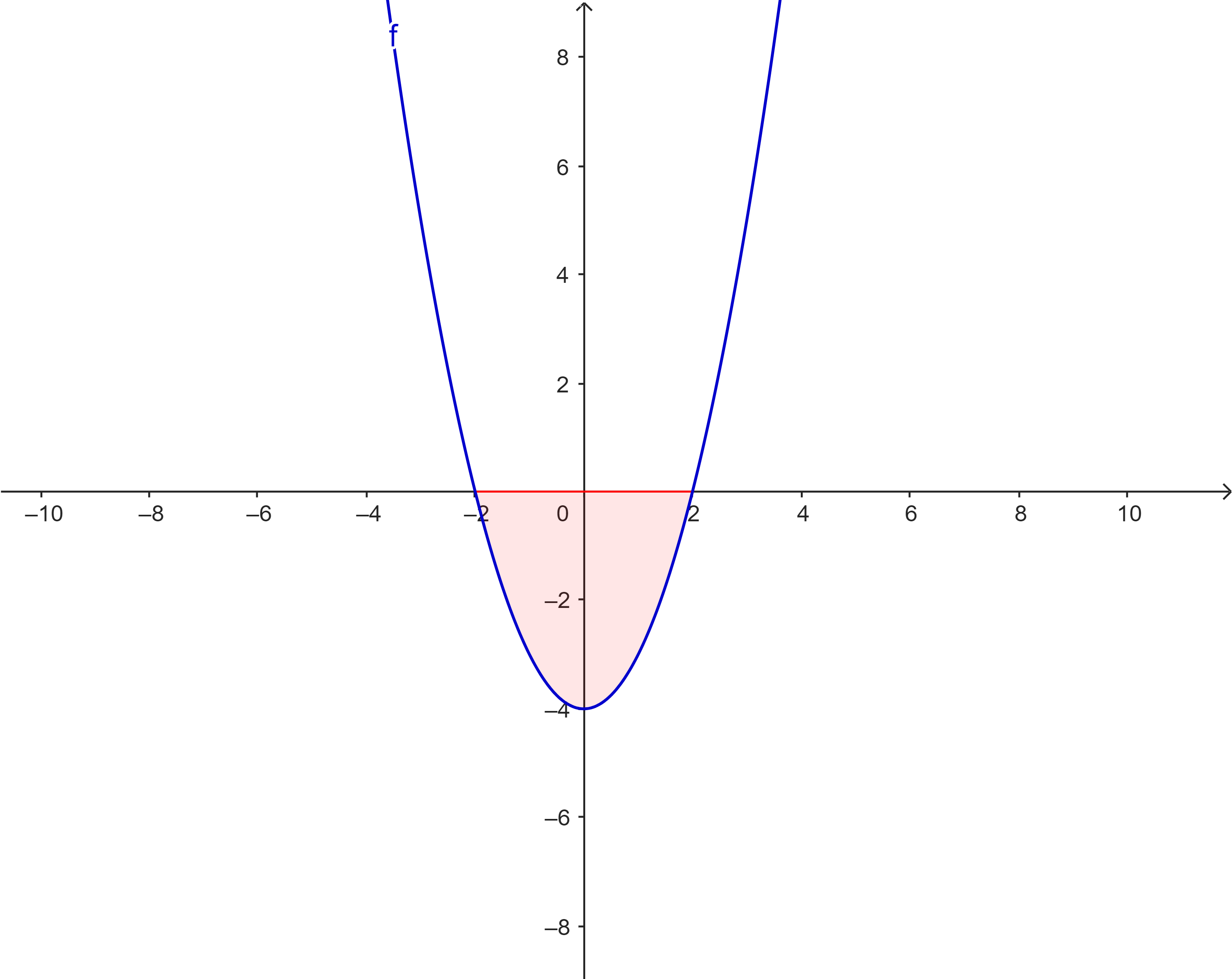
|
| (b) |
$f(x) = x^3 + x^2 - 4x - 4$ |
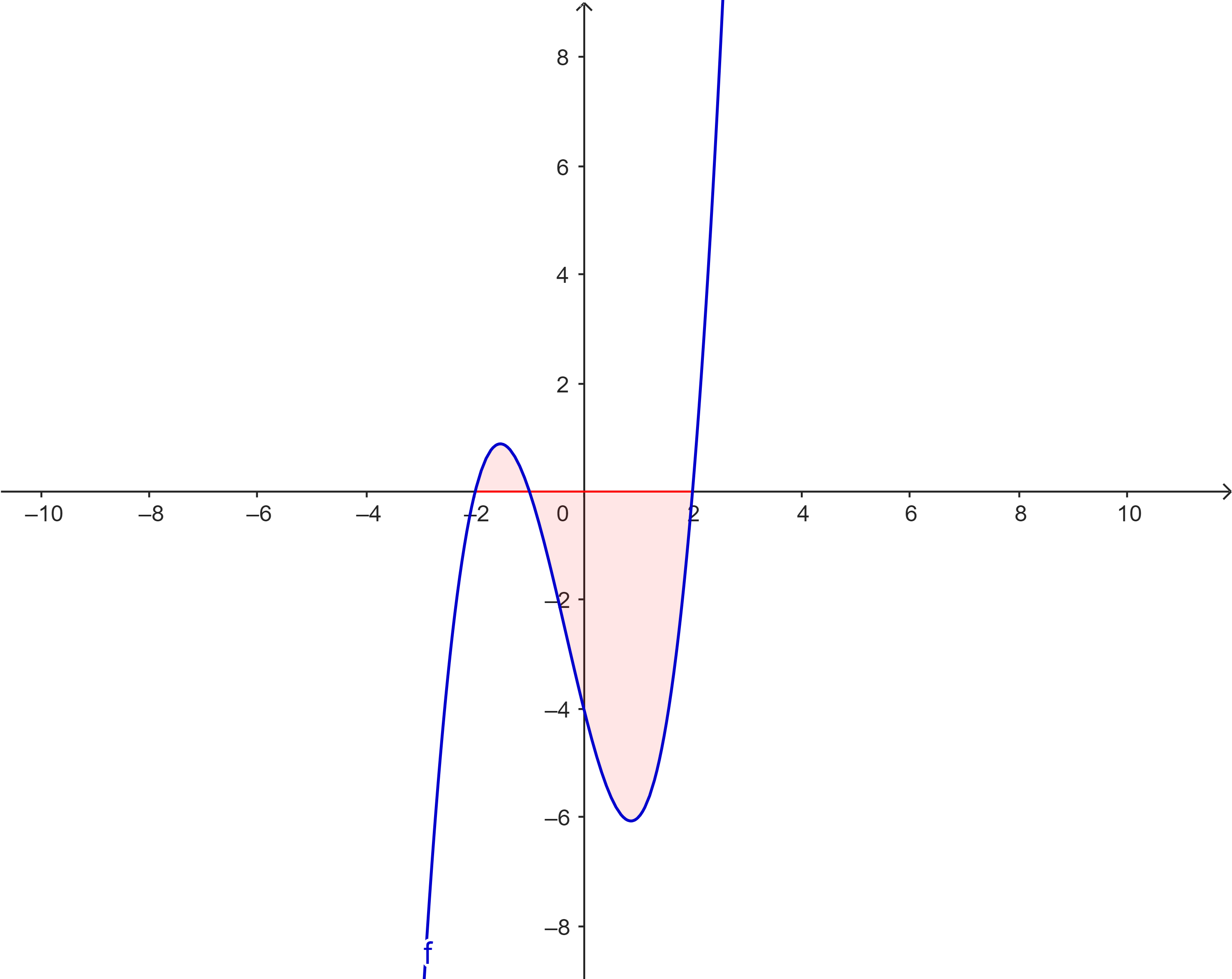
|
| (c) |
$f(x) = x^2$ $g(x) = 4$ |
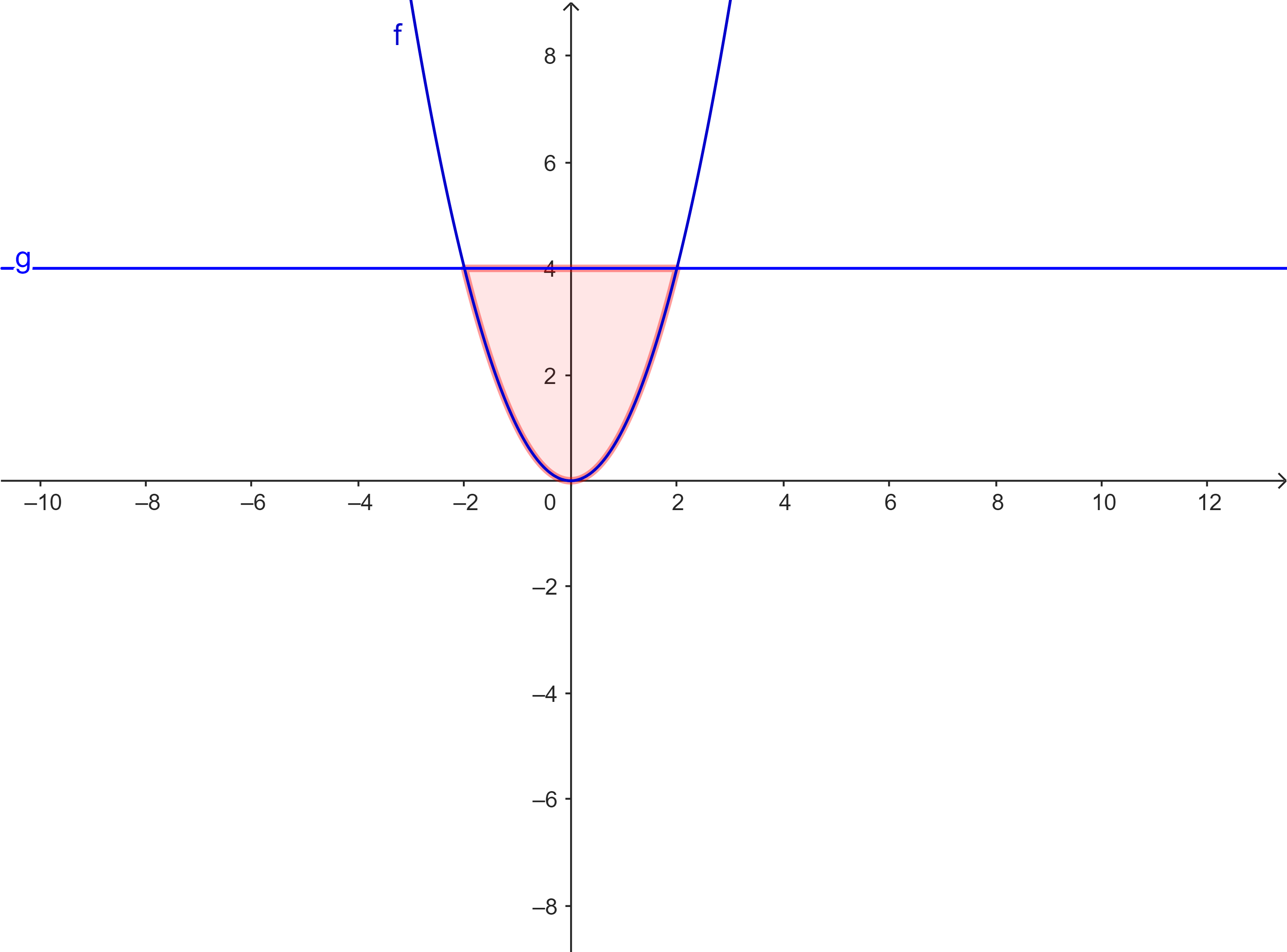
|
| (d) |
$f(x) = x^2$ $g(x) = 2x$ |
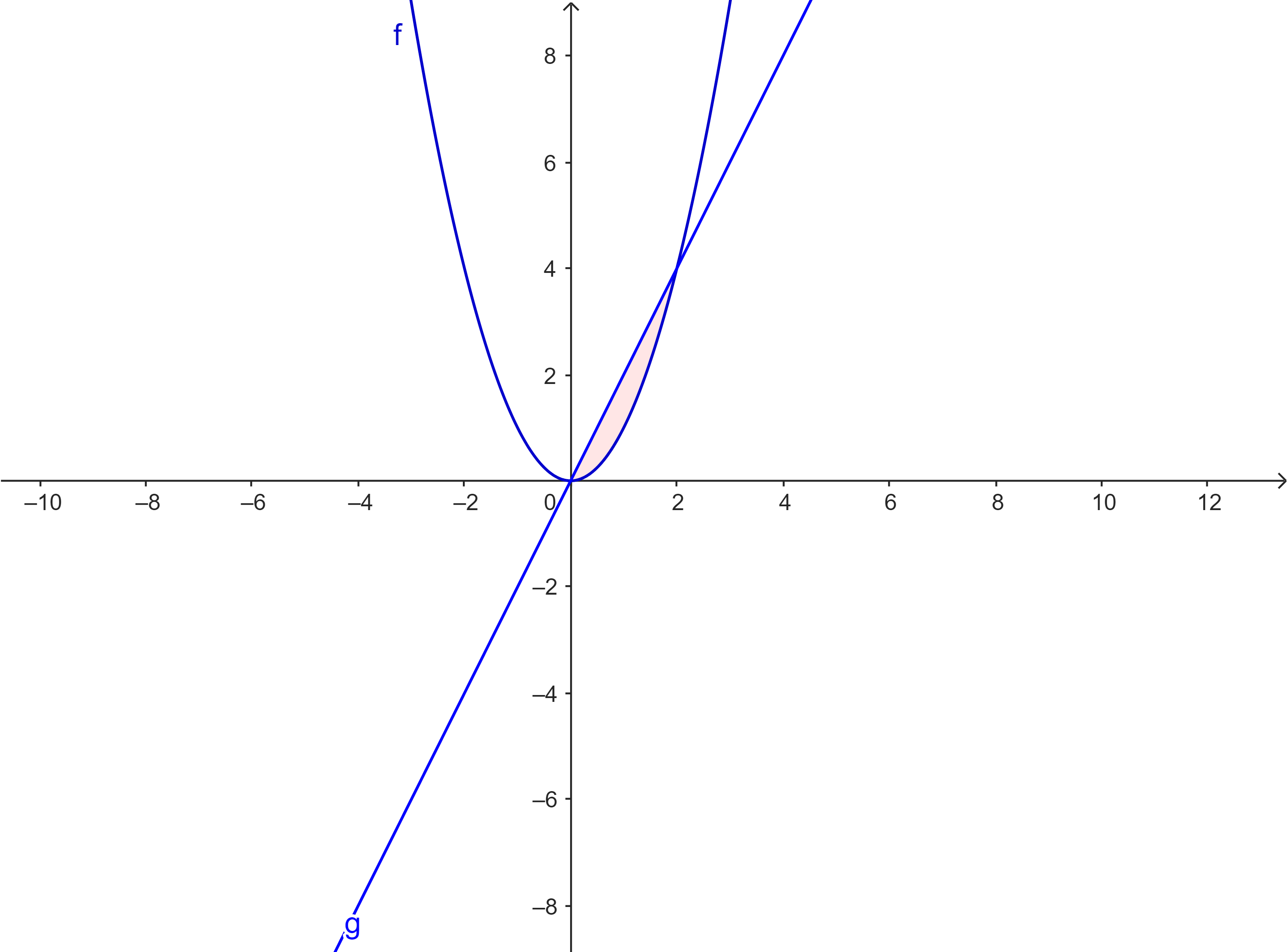
|
| (e) |
$f(x) = x^2$ $g(x) = (x-1)^2 + 1$ $h(x) = (x+1)^2 + 1$ |
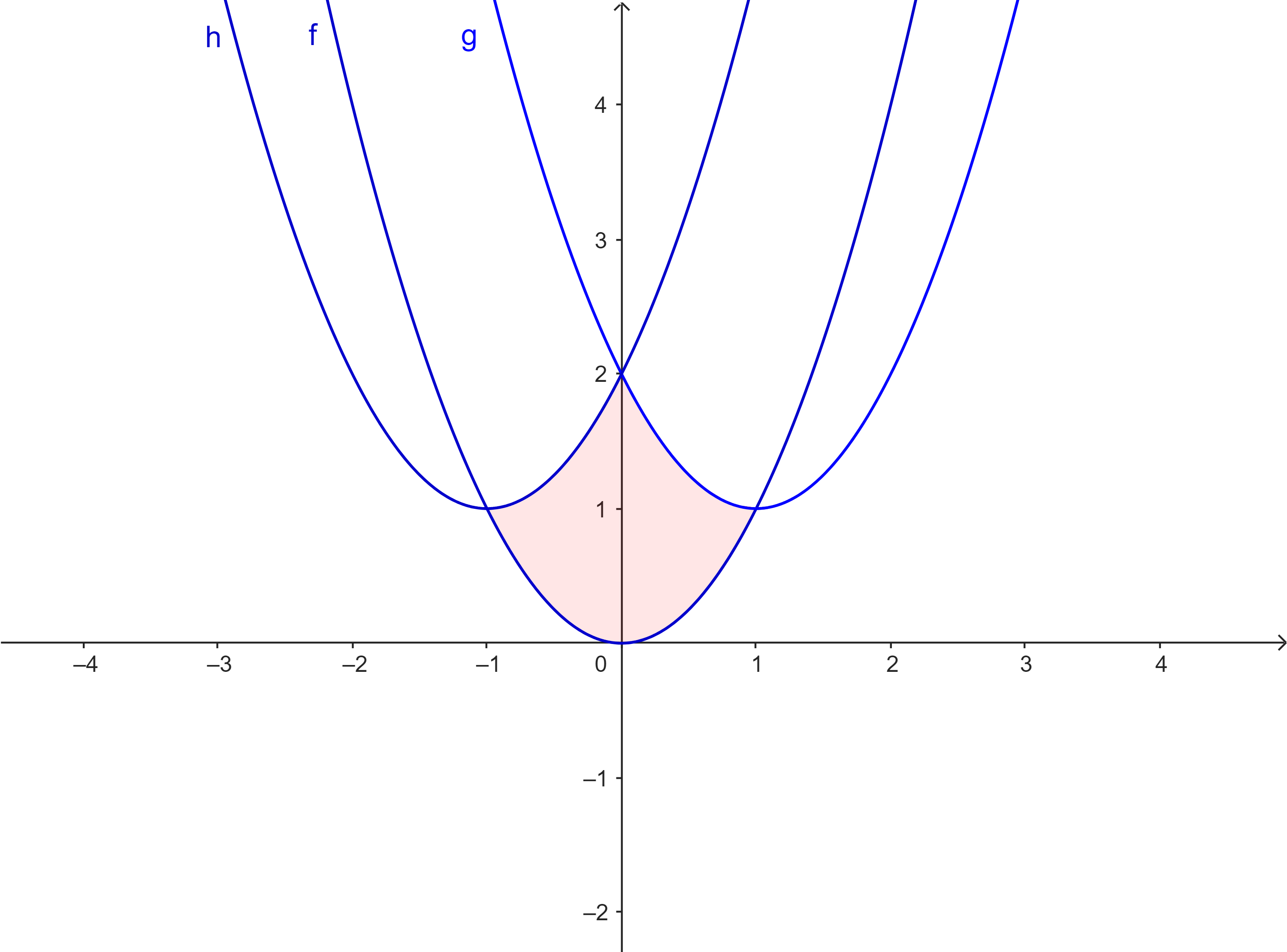
|
| (f) |
$f(x) = - \frac{1}{2}x^2 + 2x$ $g(x) = x^3 - 6x^2 + 9x$ |
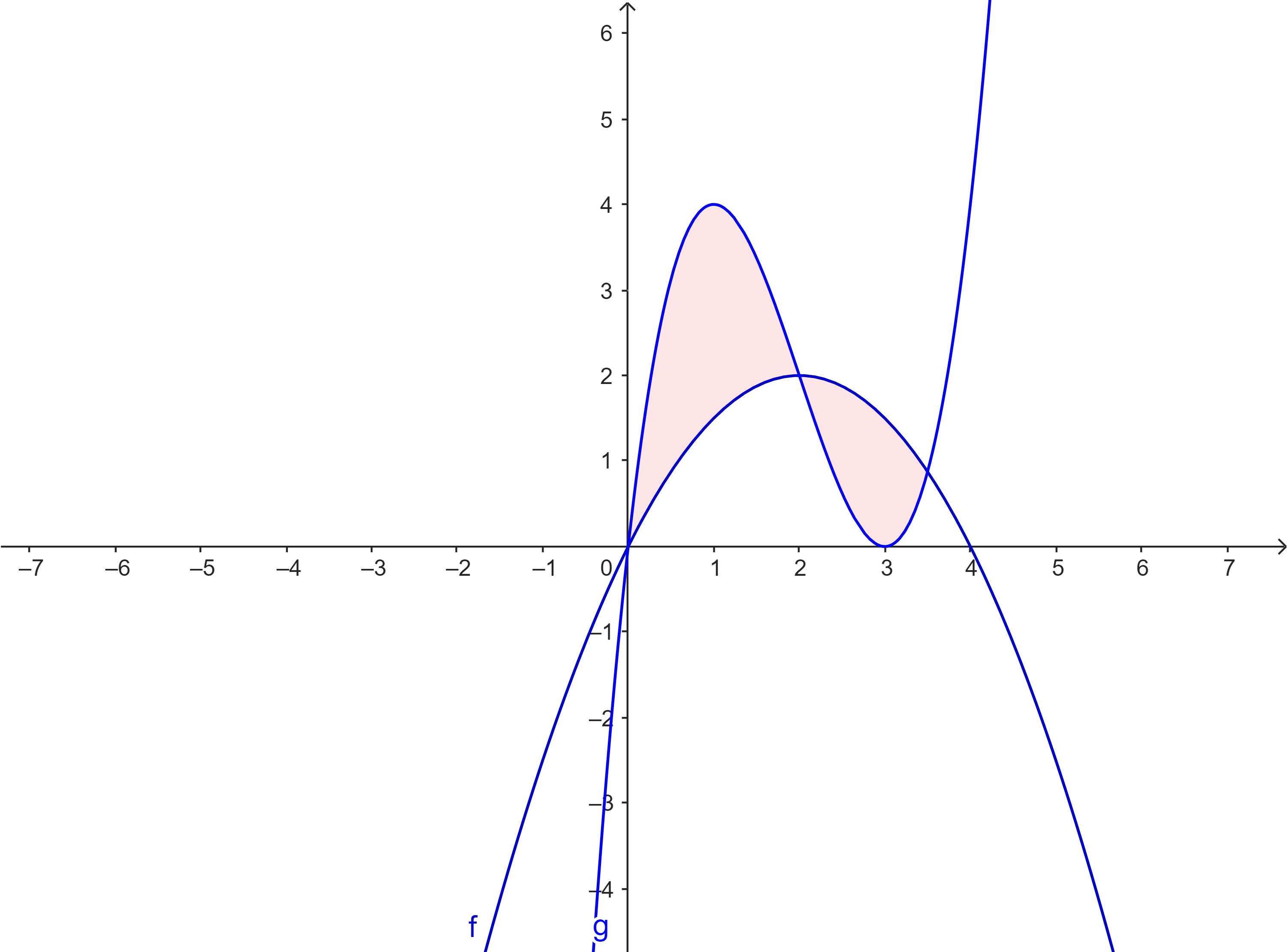
|
| (g) |
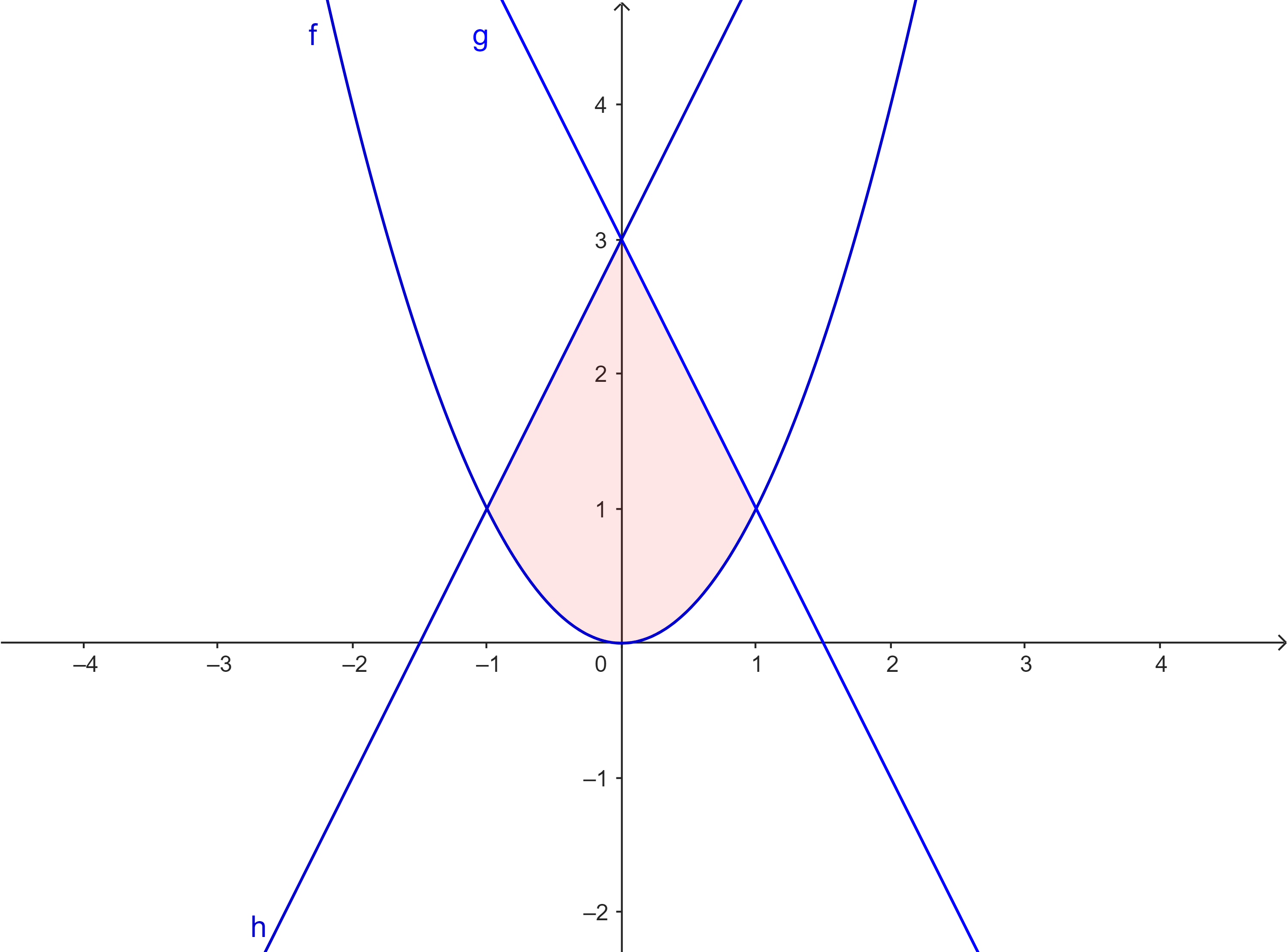
$f(x) = x^2$ $g(x) = 2(x-1) + 1$ $h(x) = -2(x+1) + 1$ |
|
| (h) |
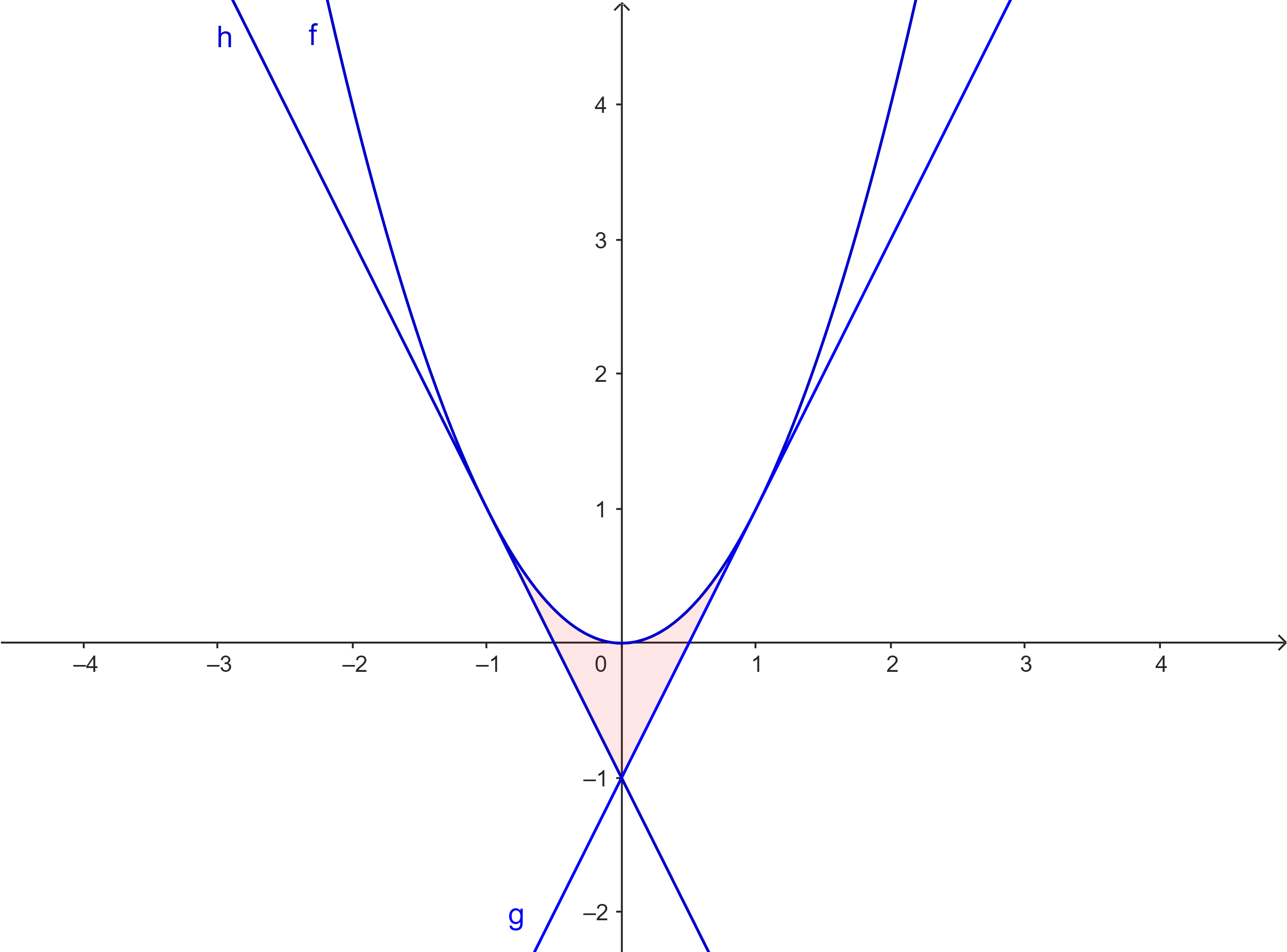
$f(x) = x^2$ $g(x) = -2(x-1) + 1$ $h(x) = 2(x+1) + 1$ |
|
Hilfsmittel: Gleichungstool
Zum Herunterladen: gleichungstool.ggb
🔑 Integralrechner zur Überprüfung
Zum Herunterladen: integralrechner.ggb

