Weitere Etagen
Die Würfelhauswelt erkunden
Nutze die Seite BlockCAD, um das Würfelhaus mit allen Etagen zu erkunden. Importiere hierzu die Datei wuerfelhaus3.xml. Mit dem Button [Rendern] erhältst du die aktuelle Würfelhauswelt. Durch Drehen und Kippen kannst du dir diese Würfelhauswelt genauer anschauen.
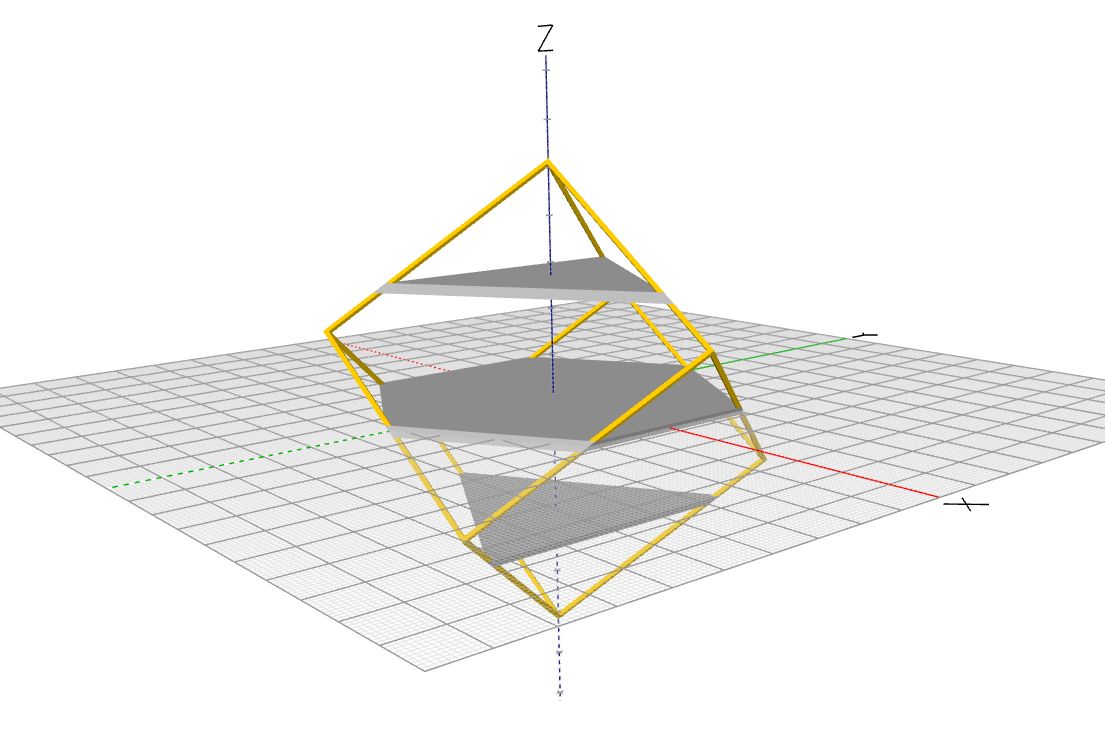
Aufgabe 1
Wie werden die weiteren Etagen erzeugt? Kanst du das aus der Würfelhausansicht erschließen? Erläutere die Konstruktion.
Die Deckenplatte mathematisch darstellen
Die Konstruktion der Deckenplatte erfolgt so: Der Punkt $D1$ teilt die Kante $FG$ im Verhältnis $1:3$ (d.h., $D1$ entsteht, indem man die Mitte der Kante $FG$ bestimmt und die Kantenhälfte bei $F$ nochmal halbiert. Die Punkte $D2$ und $D3$ erhält man analog.
Auf die analoge Konstruktion der Kellerplatte verzichten wir hier, um die Darstellung möglichst übersichtlich zu halten.
Zum Herunterladen: wuerfelhaus3.ggb
Aufgabe 2
(a) Die Punkte $D1$, $D2$ und $D3$ legen eine Ebene $E_D$ fest. Beschreibe diese Ebene mit geeigneten Ebenengleichungen (in PF, NF, KF).
(b) Wie kann man anhand der Ebenengleichungen in Normalenform direkt ersehen, dass die beiden Ebenen $E_B$ und $E_D$ parallel sind? Begründe.
So erhält man die Koordinaten von $D1$: $\overrightarrow{OD1} = \overrightarrow{OF} + \frac{1}{4} \overrightarrow{FG} = \left(\begin{array}{c} 6 \\ 0 \\ 6 \end{array}\right) + \frac{1}{4} \left(\begin{array}{c} 0 \\ 6 \\ 0 \end{array}\right) = \left(\begin{array}{c} 6 \\ 1.5 \\ 6 \end{array}\right)$
$E_D: \left[\vec{x} - \left(\begin{array}{c} 6 \\ 1.5 \\ 6 \end{array}\right)\right] \cdot \left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right) = 0$ bzw. $E_D : x_1 + x_2 + x_3 = 13.5$

