Zusammenfassung - Grenzwerte von Folgen
Stabilisierung der Folgenglieder
Die Stabilisierung der Folgenglieder ist ein Phänomen, das häufig in Anwendungssituationen auftritt. Hier ein Beispiel für eine Folge, deren Folgenglieder sich beim Grenzwert $1$ stabilisieren.
$\left( a_n \right)$: $2; 1.1; 1.001; 1.0001; 1.00001; ...$
Zur Beschreibung eines solchen Stabilisierungsverhaltens nutzt man Fachbegriffe und geeignete Schreibweisen.
Grenzwert einer Folge
Eine Folge $\left( a_n \right)$ heißt konvergent genau dann, wenn sich die Folgenglieder mit wachsender Platznummer bei einer festen reellen Zahl $g$ stabilisieren. Diese Zahl $g$ nennt man dann Grenzwert der Folge.
Eine Folge $\left( a_n \right)$ heißt divergent genau dann, wenn sie nicht konvergent ist (bzw. keinen Grenzwert hat).
Wenn eine Folge $\left( a_n \right)$ den Grenzwert $g$ hat, dann beschreiben wir dieses Grenzverhalten informell mit $a_n \rightarrow g$ (für $n \rightarrow \infty$) oder ganz formal mit dieser Schreibweise:.
$\lim\limits_{n \rightarrow \infty}{a_n} = g$
Gelesen wird das so: "Der Limes (bzw. Grenzwert) von $a_n$ für $n$ gegen Unendlich ist gleich $g$".
Beispiele
Die Beispiele in der folgenden Übersicht zeigen verschiedene Möglichkeiten konvergenter und divergenter Folgen auf.
| Folge $\left( a_n \right)$ | Grenzwert |
|---|---|
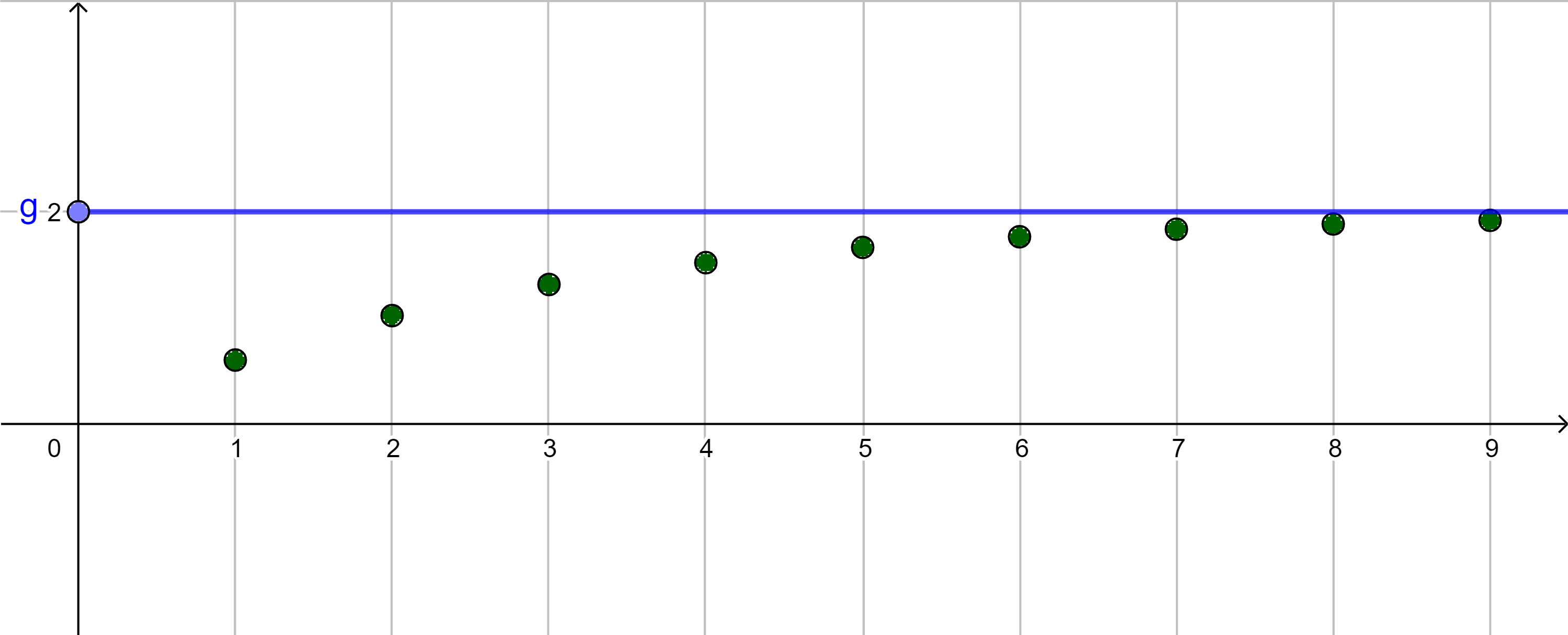
|
konvergent $a_n \rightarrow 2$ bzw. $\lim\limits_{n \rightarrow \infty}{a_n} = 2$ |
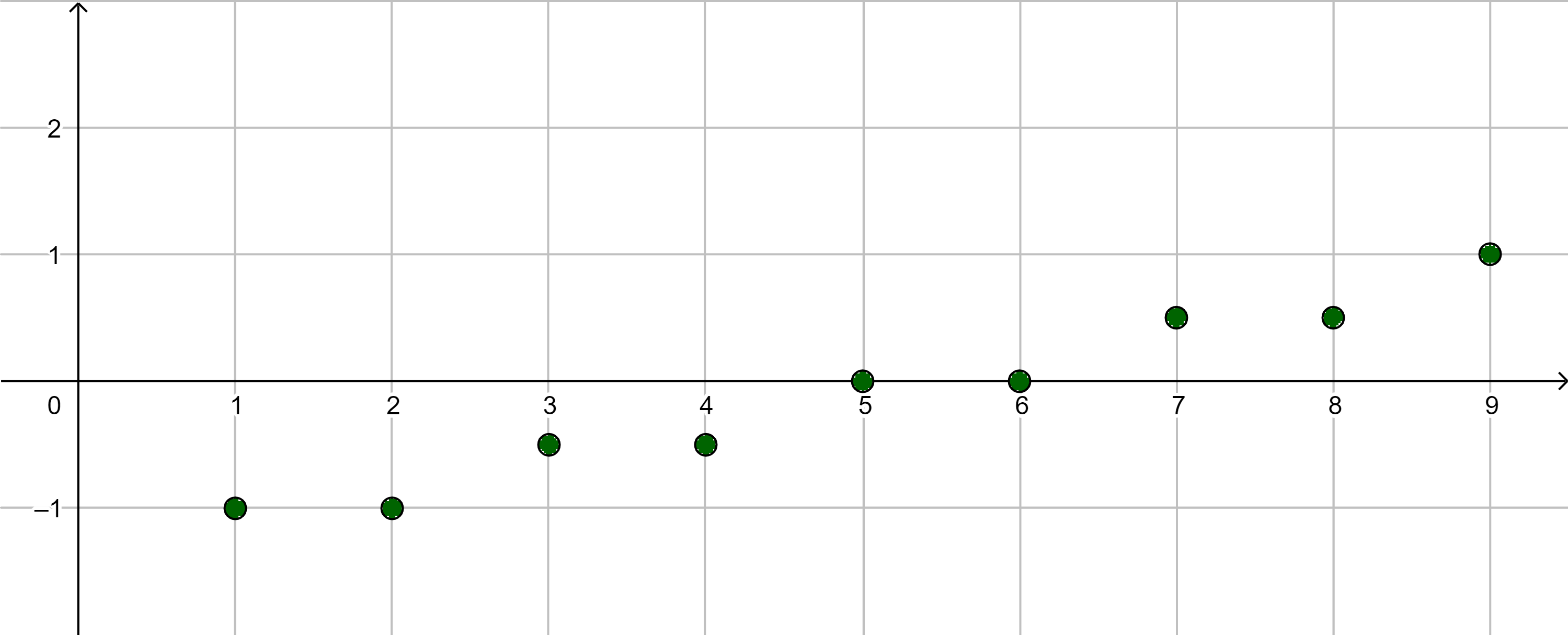
|
divergent $g$ ex. nicht |
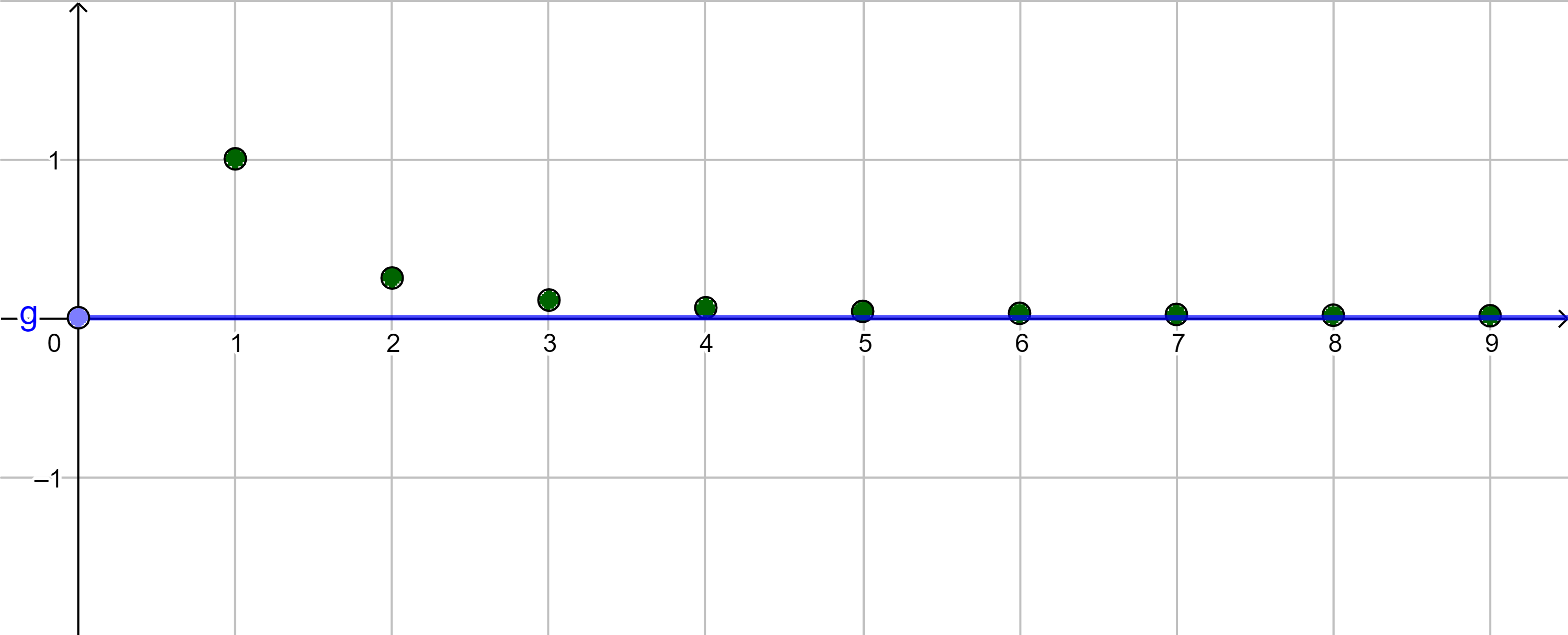
|
konvergent $a_n \rightarrow 0$ bzw. $\lim\limits_{n \rightarrow \infty}{a_n} = 0$ |
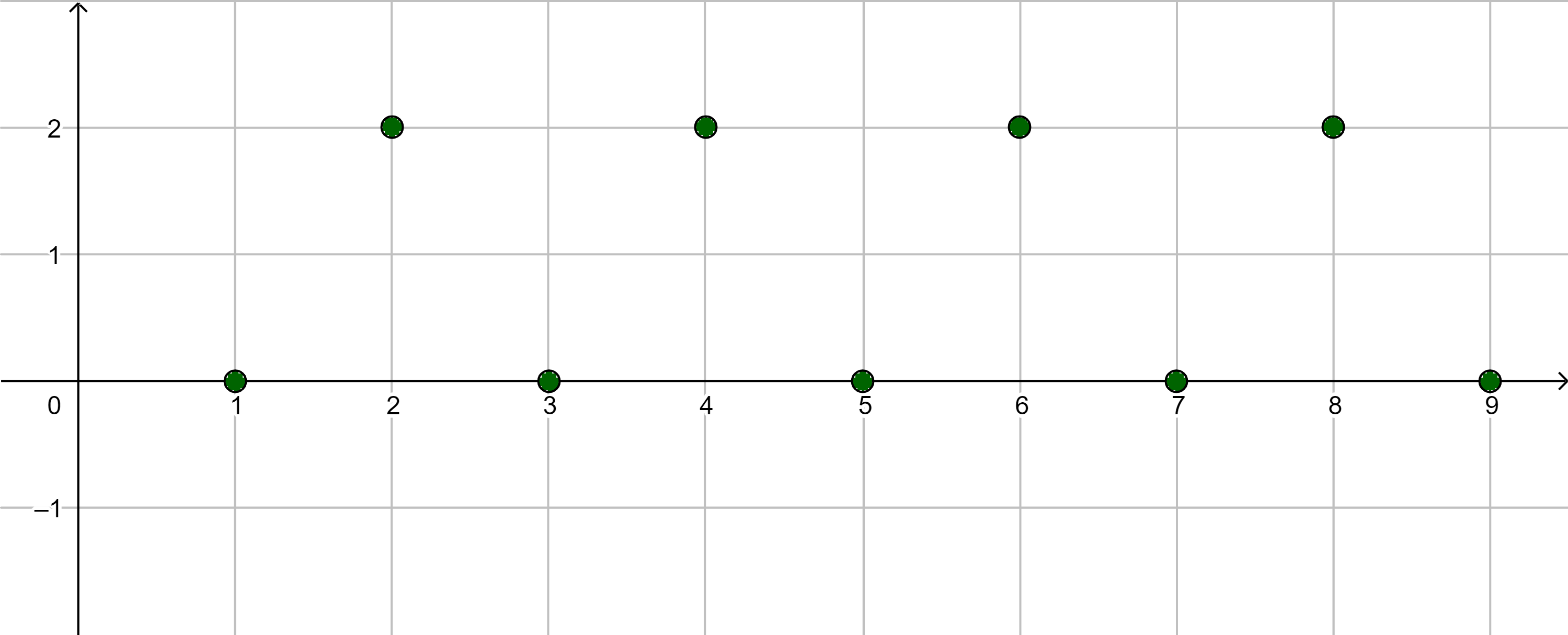
|
divergent $g$ ex. nicht |
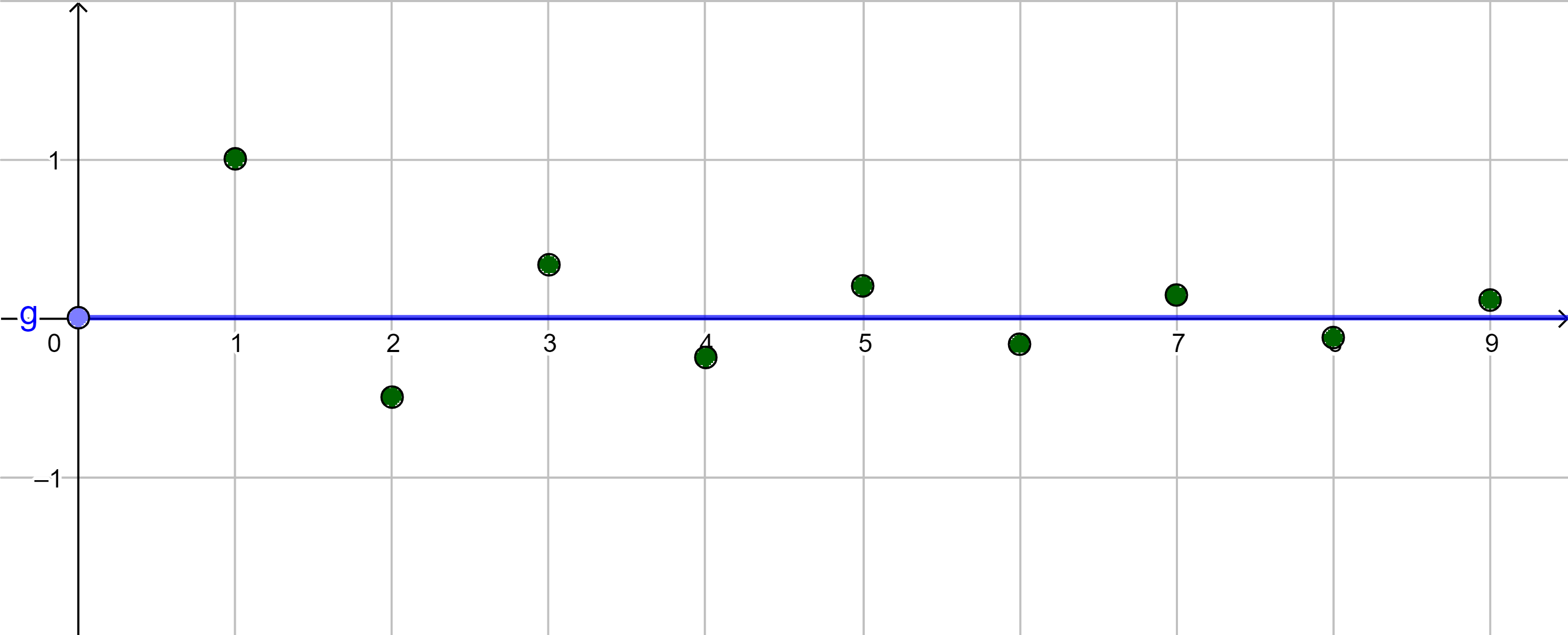
|
konvergent $a_n \rightarrow 0$ bzw. $\lim\limits_{n \rightarrow \infty}{a_n} = 0$ |
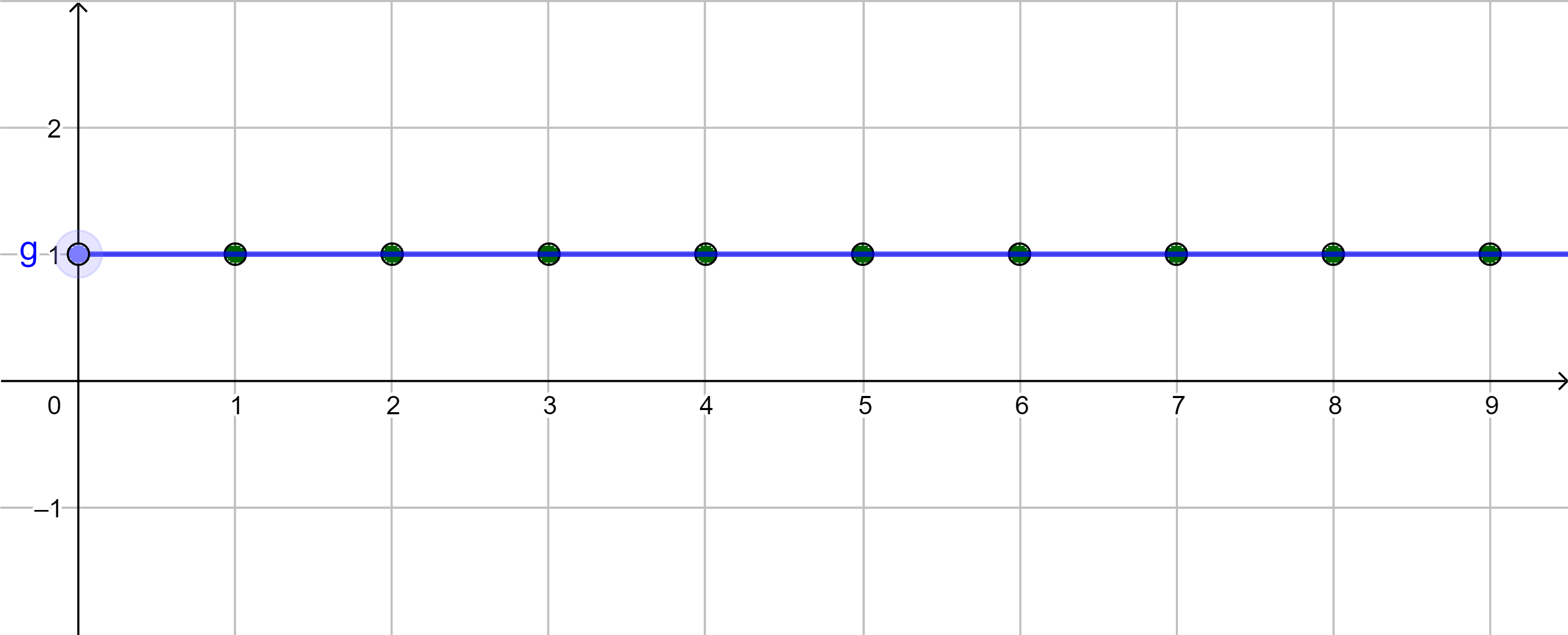
|
konvergent $a_n \rightarrow 1$ bzw. $\lim\limits_{n \rightarrow \infty}{a_n} = 1$ |
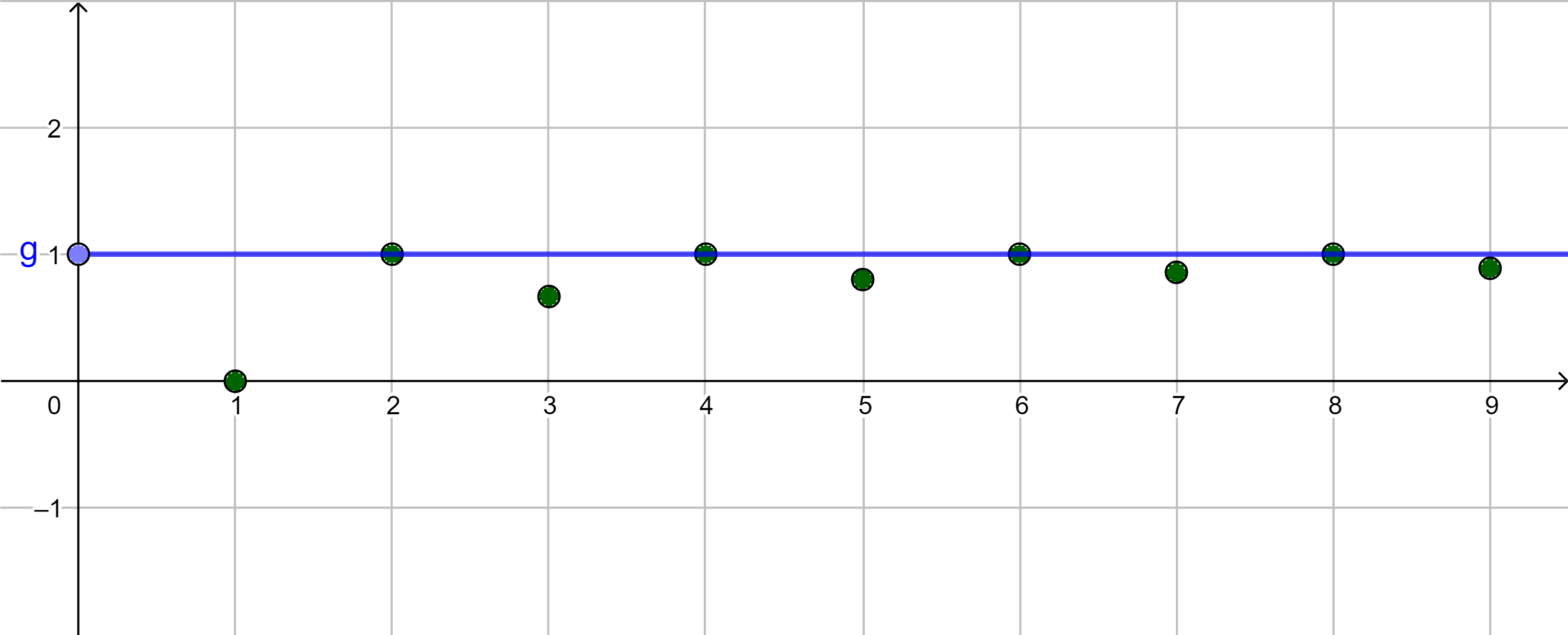
|
konvergent $a_n \rightarrow 1$ bzw. $\lim\limits_{n \rightarrow \infty}{a_n} = 1$ |
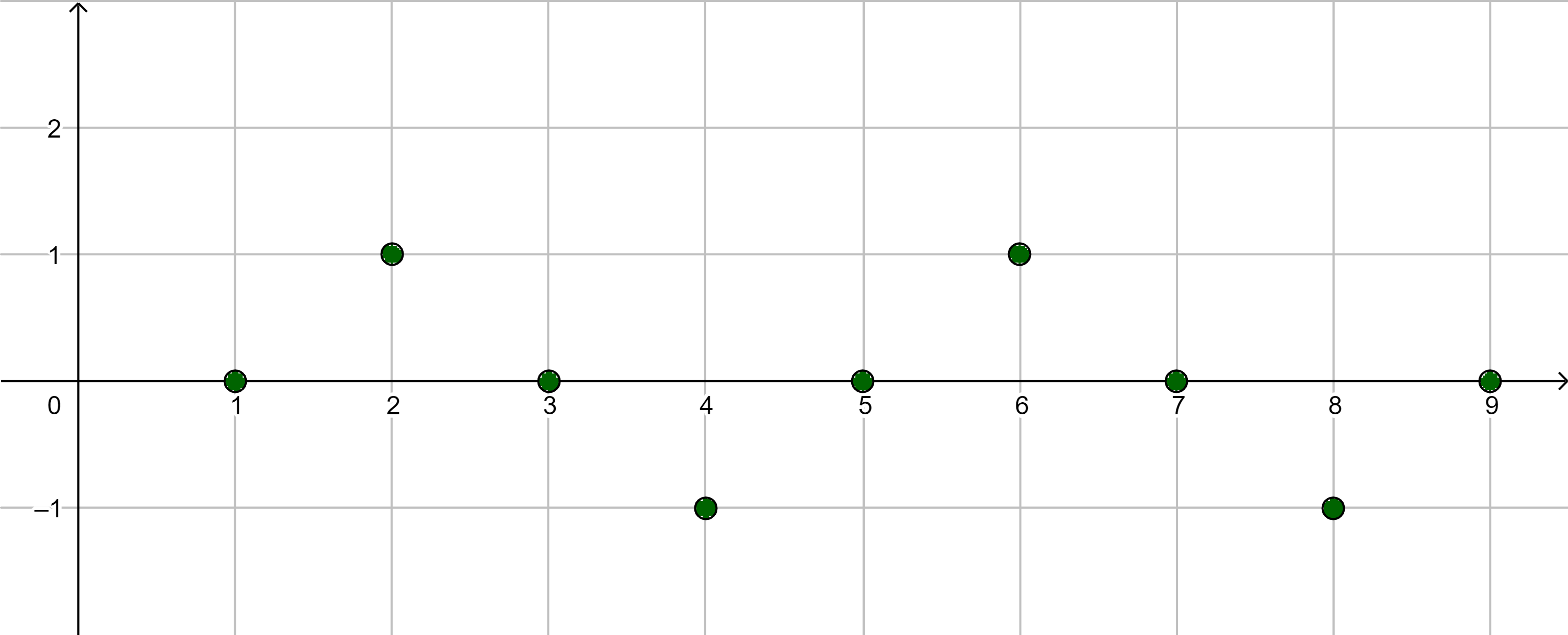
|
divergent $g$ ex. nicht |
Speziall - Nullfolgen
Nullfolge
Eine Folge $\left( a_n \right)$ heißt Nullfolge genau dann, wenn sie den Grenzwert $0$ hat.
$a_n = \displaystyle{\frac{1}{n}}$; $a_n = \displaystyle{\frac{1}{n^2}}$; $a_n = \displaystyle{\frac{1}{n^3}}$; $a_n = \displaystyle{\frac{1}{n^{0.5}}} = \displaystyle{\frac{1}{\sqrt{n}}}$; $a_n = \displaystyle{\frac{1}{n^{0.2}}}$; ...
$a_n = {0.5}^n$; $a_n = {0.1}^n$; $a_n = {0.9}^n$; $a_n = {(-0.5)}^n$; ...
Mit Hilfe von Nullfolgen lassen sich leicht konvergente Folgen mit beliebigen Grenzwerten konstruieren.
- $\lim\limits_{n \rightarrow \infty}{\left(2 + \frac{1}{n} \right)} = 2$
- $\lim\limits_{n \rightarrow \infty}{\left(1 + {0.1}^n \right)} = 1$
- $\lim\limits_{n \rightarrow \infty}{\left(-1 - {(-0.5)}^n \right)} = -1$
- $\lim\limits_{n \rightarrow \infty}{\left(3 + \frac{1}{\sqrt{n}} \right)} = 3$
Allgemein gilt:
Konstruktion konvergenter Folgen
Wenn $\left( h_n \right)$ eine Nullfolge ist und $c$ eine beliebige reelle Zahl, dann hat die Folge $\left( a_n \right)$ mit $a_n = c + h_n$ den Grenzwert $c$.
Wenn $\left( h_n \right)$ eine Nullfolge ist und $c$ eine beliebige reelle Zahl, dann hat die Folge $\left( a_n \right)$ mit $a_n = c - h_n$ den Grenzwert $c$.

