Zusammenfassung - Modellierung von Austauschprozessen
Vom Sharing-System zu Austauschprozessen
Als Beispiel für einen Austauschprozess betrachten wir ein typisches Sharing-System. Wir gehen von folgenden Rahmenbedingungen aus:
Sharing-System
- Es gibt drei Stationen, an denen die Ausleihe und Rückgabe der Tablets erfolgt. Die drei Stationen werden mit A, B und C bezeichnet.
- Ein Tablet kann nur für einen Tag ausgeliehen werden. Das Tablet kann an einer beliebigen Station ausgeliehen und an einer beliebigen Station wieder zurückgegeben werden.
- Es werden 300 Tablets zur Verfügung gestellt. Diese werden zu Beginn auf die drei Stationen aufgeteilt (also: 100 Tablets an jede Station).
- Wir gehen beim betrachteten Sharing-System davon aus, dass die täglichen Übergangsraten in etwa gleich sind. Der folgende Übergangsgraph gibt die jeweigen Übergangsraten an.
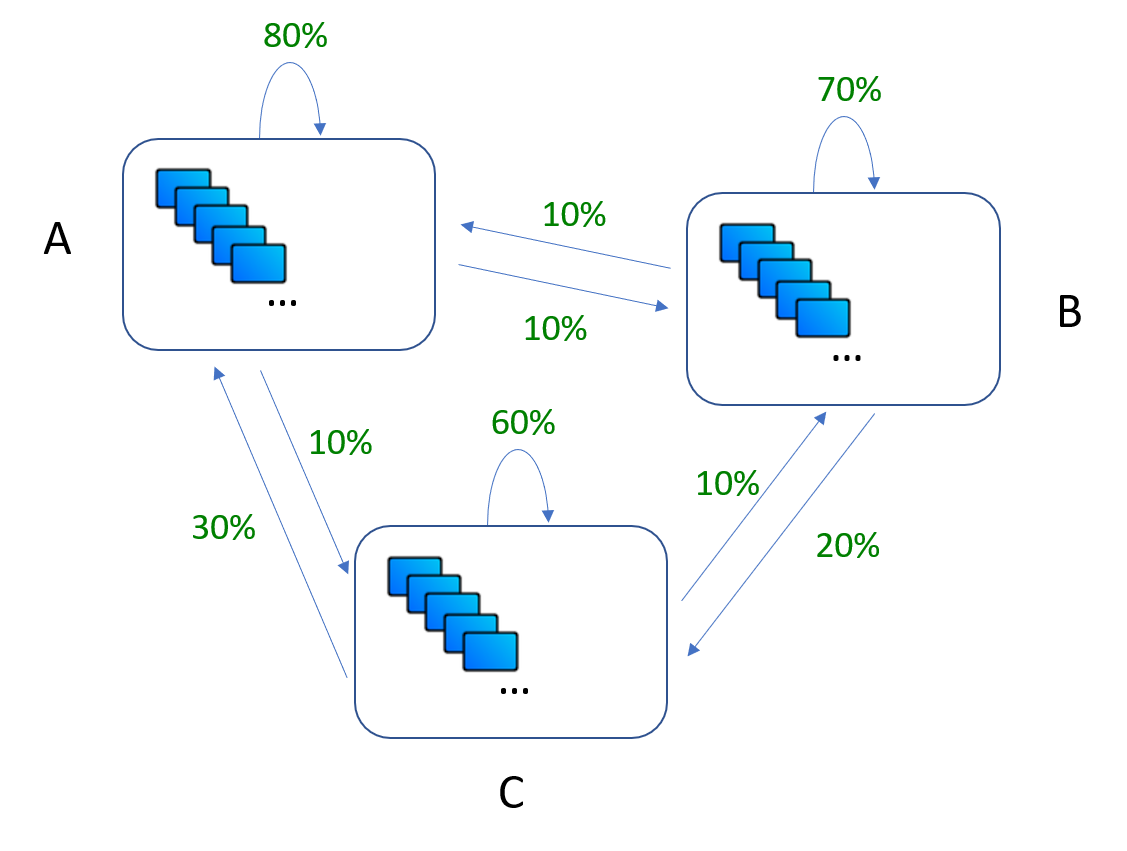
- Der Übergangsgraph ist so zu lesen: Durchschnittlich $10 \%$ der Tablets, die in A ausgeliehen werden, werden in B zurückgegeben. Durchschnittlich $10 \%$ der Tablets, die in A ausgeliehen werden, werden in C zurückgegeben. Durchschnittlich $80 \%$ der Tablets in A verbleiben in A. Sie werden entweder nicht ausgeliehen oder wieder in A zurückgegeben. ...
Anhand dieses Sharing-Systems kann man bereits typische Merkmale eines Austauschprozess erkennen.
Austauschprozess
Bei einem Austauschprozess betrachtet man die Entwicklung eines Bestandes an Objekten (wie z.B. Tablets). Die Objekte können sich dabei in verschiedenen Zuständen befinden (bei den Tablets legt der Ort, an dem sie gelagert sind, den jeweiligen Zustand fest). Während des Prozesses ändert sich die Gesamtanzahl der Objekte nicht. Es ändert sich lediglich die Verteilung der Objekte hinsichtlich ihrer Zustände.
Modellierung und Simulation eines Austauschprozesses
Wir gehen vom oben informell beschriebenen Sharing-System aus. Die Systembeschreibung erfolgt mit einem Übergangsgraph, in dem sämtliche Übergangsraten eingetragen sind. Die Prozessentwicklung lässt sich mit einer Entwicklungstabelle verdeutlichen. Die Zahlen in der Entwicklungstabelle beschreiben die jeweilige Verteilung der Obkekte auf die Zustände. Vorgeben muss man nur die Ausgangsverteilung. Die weiteren Verteilungen ergeben sich dann mit Hilfe der Übergangsraten.
Beachte, dass wir in einer Entwicklungstabelle auch Dezimalzahlen als Verteilungswerte zulassen.
In der realen Welt machen Angaben wie $80.4$ Tablets
keinen Sinn.
Die Verteilungswerte sind Modellwerte, die die reale Situationen nur näherungsweise beschreiben.
Sharing-System-Modell
| Systembeschreibung mit einem Übergangsgraph | Prozessentwicklung mit einer Entwicklungstabelle | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Entscheidend für die Prozessentwicklung sind die Zahlenangaben an den Kanten des Übergangsgraphen. Diese Zahlen geben die Anteile der Objekte an, die im nächsten Simulationsschritt vom ausgehenden Zustand in den hinführenden Zustand wechseln.
Damit die Gesamtanzahl der Objekte im Austauschprozess gleich bleibt, müssen die Übergangsraten im Übergangsgraph folgende Bedingung erfüllen:
Bedingung an Übergangsraten bei einem Austauschprozess
Im Übergangsgraph muss die Summe aller Übergangsraten an den Kanten, die von einem Knoten ausgehen, den Wert $1$ ergeben.
Systemmodellierung mit einer Matrix
Die gesamte Information eines Übergangsgraphen zu einem Austauschprozess kann man auch mit Hilfe einer Übergangstabelle darstellen. Die Übergangstabelle kann man dann als Matrix deuten. Diese Matrix wird Prozessmatrix (odeer auch Übergangsmatrix) genannt.
Sharing-System: Systembeschreibung
| Übergangsgraph | Übergangstabelle | Prozessmatrix | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
$P = \begin{pmatrix} 0.8 & 0.1 & 0.3 \\ 0.1 & 0.7 & 0.1 \\ 0.1 & 0.2 & 0.6 \end{pmatrix}$ |
Die Prozessmatrix bei einem Austauschprozess muss
– genau wie der entsprechende Übergangsgraph – bestimmte Bedingungen erfüllen.
Man erfasst diese Bedingungen mit dem Begriff stochastische Matrix
.
Stochastische Matrix
Eine stochastische Matrix ist eine Matrix mit folgenden Eigenschaften:
- Die Matrix ist quadratisch.
- Alle Elemente $a_{ij}$ der Matrix sind reelle Zahlen mit $0 \leq a_{ij} \leq 1$.
- Die Summe aller Elemente in jeder Spalte der Matrix beträgt $1$.
Beschreibung von Objektverteilungen mit Vektoren
Die jeweilige Aufteilung eines Objektbestandes in die Zustände beschreibt man bei Austauschprozessen mit Verteilungsvektoren.
Sharing-System: Prozessentwicklung mit Verteilungsvektoren
| Übergangsgraph | Prozessmatrix | Veteilungsvektor |
|---|---|---|
|
|
$P = \begin{pmatrix} 0.8 & 0.1 & 0.3 \\ 0.1 & 0.7 & 0.1 \\ 0.1 & 0.2 & 0.6 \end{pmatrix}$ | $\vec{v} = \begin{pmatrix} 100 \\ 100 \\ 100 \end{pmatrix}$ |
Häufig wird – wie in der Übersicht oben – die Aufteilung des Objektbestandes mit einem Verteilungsvektor mit absoluten Häufigkeitsangaben erfasst. Die Elemente des solchen absoluten Verteilungsvektors geben an, wie viele Objekte sich aktuell in den betreffenden Zuständen befinden. Die Summe der Elemente eines aktuellen Verteilungsvektors gibt dann die Gesamtzahl der Objekte an. Da wir keine leeren Objektbestände betrachten, kommt der Nullvektor nicht als absoluter Verteilungsvektor in Betracht.
Oft ist es sinnvoll, die Aufteilung des Objektbestandes mit relativen Häufigkeitsangaben zu beschreiben. Jedes Element eines solchen relativen Verteilungsvektors beschreibt dann den Anteil des Objektbestandes im betreffenden Zustand. Die Summe der Elemente eines relativen Verteilungsvektors muss $1$ (bzw. $100 \%$) ergeben.
Prozessentwicklung mit dem Matrix-Vektor-Produkt
Bei der Ausführung eines Austauschprozesses werden ausgehend von einer Ausgangsverteilung in jedem Schritt die neuen Verteilungen der Objekte auf die Zustände bestimmt. Im Tablet-Sharing-System erhält man folgende Werte:
| Schritte | A | B | C |
|---|---|---|---|
| $0$ | $100$ | $100$ | $100$ |
| $1$ | $\begin{array}{lcl} 120 & = & 0.8 \cdot 100 \\ & + & 0.1 \cdot 100 \\ & + & 0.3 \cdot 100 \end{array}$ | $\begin{array}{lcl} 90 & = & 0.1 \cdot 100 \\ & + & 0.7 \cdot 100 \\ & + & 0.1 \cdot 100 \end{array}$ | $\begin{array}{lcl} 90 & = & 0.1 \cdot 100 \\ & + & 0.2 \cdot 100 \\ & + & 0.6 \cdot 100 \end{array}$ |
| $2$ | $\begin{array}{lcl} 132 & = & 0.8 \cdot 120 \\ & + & 0.1 \cdot 90 \\ & + & 0.3 \cdot 90 \end{array}$ | $\begin{array}{lcl} 84 & = & 0.1 \cdot 120 \\ & + & 0.7 \cdot 90 \\ & + & 0.1 \cdot 90 \end{array}$ | $\begin{array}{lcl} 84 & = & 0.1 \cdot 120 \\ & + & 0.2 \cdot 90 \\ & + & 0.6 \cdot 90 \end{array}$ |
| ... | ... | ... | ... |
Diese Berechnungen kann man übersichtlich mit den Matrix-Vektor-Produkt darstellen.
| Schritte | Verteilungsvektor | Berechnung |
|---|---|---|
| $0$ | $\vec{v}_0 = \begin{pmatrix} 100 \\ 100 \\ 100 \end{pmatrix}$ | |
| $1$ | $\vec{v}_1 = \begin{pmatrix} 120 \\ 90 \\ 90 \end{pmatrix}$ | $\vec{v}_1 = P \cdot \vec{v}_0 = \begin{pmatrix} 0.8 & 0.1 & 0.3 \\ 0.1 & 0.7 & 0.1 \\ 0.1 & 0.2 & 0.6 \end{pmatrix} \cdot \begin{pmatrix} 100 \\ 100 \\ 100 \end{pmatrix}$ |
| $2$ | $\vec{v}_2 = \begin{pmatrix} 132 \\ 84 \\ 84 \end{pmatrix}$ | $\vec{v}_2 = P \cdot \vec{v}_1 = \begin{pmatrix} 0.8 & 0.1 & 0.3 \\ 0.1 & 0.7 & 0.1 \\ 0.1 & 0.2 & 0.6 \end{pmatrix} \cdot \begin{pmatrix} 120 \\ 90 \\ 90 \end{pmatrix}$ |
| ... | ... | ... |
| $n$ | $\vec{v}_n = \cdots$ | $\vec{v}_n = P \cdot \vec{v}_{n-1}$ |
Man erhält so folgendes Verfahren zur Simulation eines Austauschprozesses.
Simulation eines Austauschprozesses
Ein Austauschprozess werde mit einer Prozessmatrix $P$ beschrieben. Die Ausgangsverteilung der Objekte werde mit einem Verteilungsvektor $\vec{v}_{0}$ beschrieben. Die Entwicklung der Objektverteilungen kann man dann so berechnen:
$\vec{v}_n = P \cdot \vec{v}_{n-1}$ für alle Schritte $n \geq 1$.

