Differenzierbarkeit

Worum geht es hier?

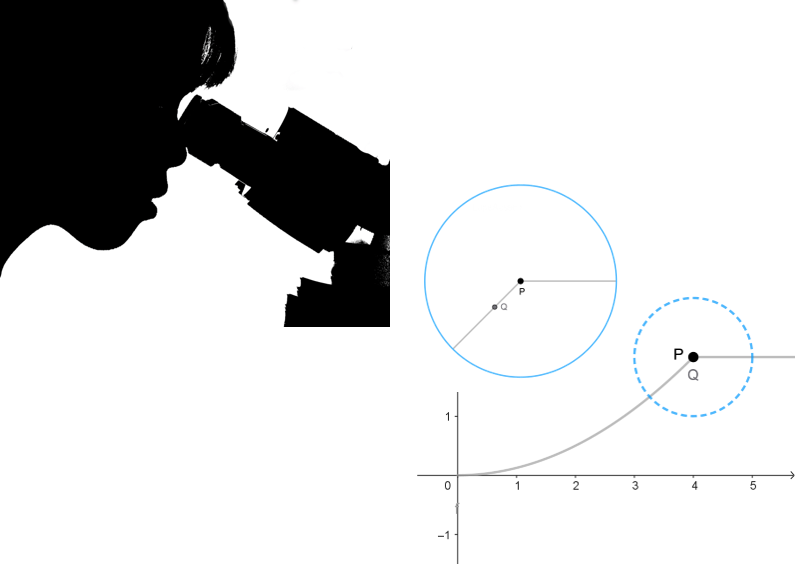
Im letzten Kapitel wurde die Ableitung als Grenzwert von mittleren Änderungsraten eingeführt. Geometrisch kann man sie als Grenzwert von Sekantensteigungen deuten. Hier geht es jetzt um die Frage, ob dieser Grenzwert immer existiert. Wir werden Funktionen betrachten, bei denen eine Grenzwertbildung nicht möglich ist.

Für dieses Thema musst du ...

• ... sicher mit Funktionen umgehen können.
• ... das Konzept der Ableitung verstanden haben.

Hier lernst du, ...

• ... was man unter Differenzierbarkeit versteht.
• ... in welchen Fällen die Ableitung an einer Stelle nicht existiert.

Hier geht's zur Konzeption des Kapitels.