Zusammenfassung – 3D-Koordinatensysteme
Positionsbeschreibung in einem Koordinatensystem
Koordinatensysteme werden sowohl in der realen Welt als auch in der abstrahierenden Mathematik benutzt, um Positionen von Objekten präzise zu beschreiben.
3D-Koordinatensystem
Ein 3D-Koordinatensystem benutzt man, um die Position von Punkten im Raum mit Hilfe von Zahlen zu beschreiben. Wir verwenden hier folgende Konventionen:
- Das Koordinatensystem besteht aus drei Achsen, mit denen man Tiefe, Breite und Höhe zu einem Bezugspunkt beschreibt.
- Die drei Achsen sind paarweise senkrecht zueinander angeordnet und schneiden sich im Ursprung (als Bezugspunkt).
- Die Achsen werden als $x_1$-Achse, $x_2$-Achse und $x_3$-Achse bezeichnet.
- Die $x_1$-Achse zeigt
nach vorne
, die $x_2$-Achsenach rechts
und die $x_3$-Achsenach oben
.
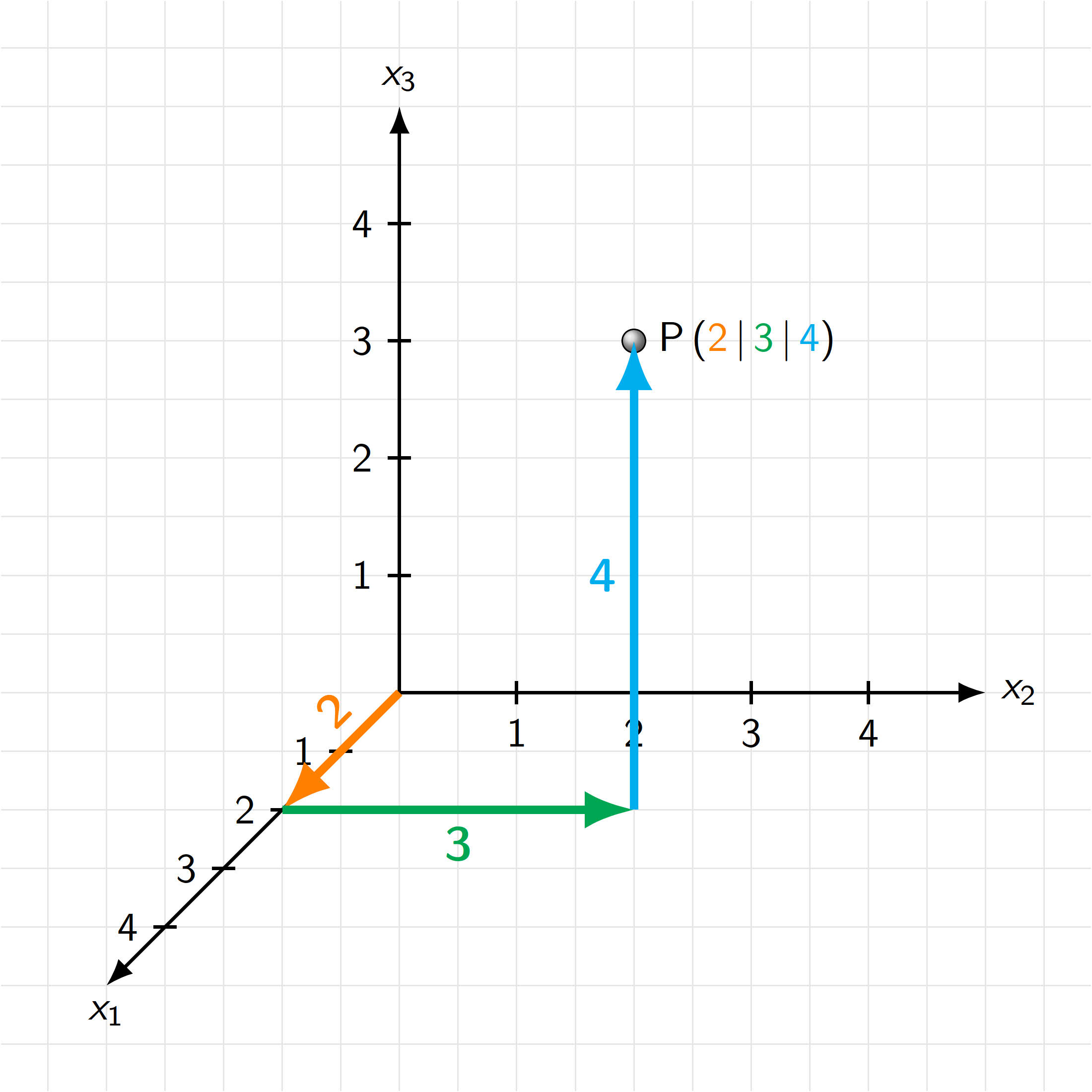
Die Lage eines Punktes kann man dann mithilfe eines Zahlentripels (Liste dreier Zahlen) darstellen. Diese Zahlen beschreiben, wie viele Einheiten man vom Ursprung aus in $x_1$-Richtung, in $x_2$-Richtung und in $x_3$-Richtung bewegen muss, um zum Punkt zu gelangen.
Geometrische Deutung von 3D-Vektoren
Vektoren werden in der 3D-Geometrie genauso verwendet wie in der 2D-Geometrie. Zur Verdeutlichung betrachten wir die Bewegung eines Raumschiffs im 3D-Raum.
Zum Herunterladen: raumschiff_bewegen.ggb
Im Applet werden Darstellungen der folgenden Art benutzt.
$\underbrace{\begin{pmatrix} -3 \\ 1 \\ 2 \end{pmatrix}}_{\text{Ausgangsposition}} \overbrace{\stackrel{\begin{pmatrix} 5 \\ 2 \\ -1 \end{pmatrix}}{\longrightarrow}}^{\text{Verschiebung}} \underbrace{\begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}}_{\text{Endposotion}}$
Sie verdeutlichen die Verwendung von Vektoren in der 3D-Geometrie:
Geometrische Deutung von 3D-Vektoren
3D-Vektoren kann man zur Beschreibung von Punkten und von Verschiebungen im 3D-Raum verwenden.

