Problemstellung
Zur Orientierung
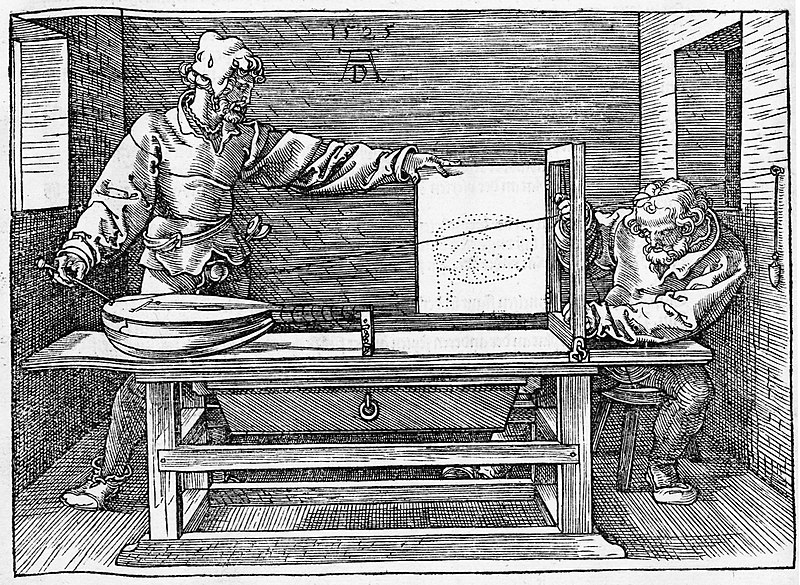
Beim Zeichnen von Weltausschnitten geht es oft darum, diese möglichst realitätsnah abzubilden. Das bedeutet, dass räumliche Strukturen auf dem Zeichenblatt so erscheinen sollen, wie ein Betrachter sie in der Realität sieht. Hierzu verwendet man die Zentralperspektive. Ein Verfahren zur Umsetzung wird im Holzschnitt von Albrecht Dürer beschrieben.
- Der Nagel an der Wand entspricht dem Augpunkt. Von diesem Punkt aus wird das 3D-Objekt betrachtet.
- Die gespannte Schnur verdeutlicht einen Lichtstrahl, der von einem Punkt eines 3D-Objekts (z.B. einer Laute) aus zum Auge des Betrachters fällt.
- Im Rahmen befindet sich die Zeichenebene. Dort, wo der Lichtstrahl die Zeichenebene trifft, wird der zum Punkt des 3D-Objekts gehörende Bildpunkt markiert.
- Wenn man diese Konstruktion für möglichst viele Punkte des 3D-Objekts durchführt, erhält man Gerüst für eine realitätsnahe Abbildung des 3D-Objekts auf die 2D-Zeichenebene.
Unser Ziel hier besteht darin, diese Konstruktion mit Hilfe einer geeigneten geometrischen Abbildung zu beschreiben.
Das Problem präzisieren
Erkunde das zu bearbeitende Problem anhand des folgenden Applets. Bearbeite hierzu die darunter aufgeführten Aufgaben.
Zum Herunterladen: projektion3_zentralperspektive_turm_zuordnungen.ggb
Aufgabe 1
Betrachte zunächst die Ausgangssituatuion.
Gegeben
- Gegeben ist eine 3D-Miniwelt. Wir betrachten einfache Welten, die aus Punkten und Kanten bestehen.
Im Applet ist ein quadratischer Turm als 3D-Minwelt bereits vorgegeben. Im Applet kann man im unteren Fenster die betrachtete 3D-Minwelt verändern und selbst konfigurieren. Hierzu muss man nur die betrachteten Punkte und Kanten in den entsprechenden Eingabefeldern eintragen. Probiere das selbst aus. Ändere die 3D-Miniwelt so ab, dass der Turm eine pyramitenförmige Spitze erhält.
Aufgabe 2
Betrachte auch die gewünschte Zielsituatuion.
Gesucht
- Gesucht ist ein Verfahren zur Erzeugung von zentralperspektivischen Bildern.
Mit dem Verfahren soll zu einem beliebigen Ausgangspunkt $X$ der zugehörige Bildpunkt $X'$ berechnet werden. Erkunde die Zusammenhänge im Applet.
- Der Augpunkt befindet sich im Ursprung des Koordinatensystems.
- Im Applet kann man im 3D-Grafikfenster den Punkt $X$ im vorgegebenen 3D-Objekt zu verschiedenen Eckpunkten bewegen. Probiere das selbst aus.
- Auf der Zeichenebene wird der Bildpunkt $X'$ erzeugt. Die Zeichenebene kann man hin und her bewegen. Hierdurch verändert man den Abstand $d$ zum Augpunkt.
- Im oberen rechten Fenster wird die jeweilige Zuordnung $\alpha: \underbrace{\vec{x}}_{X} \rightarrow \underbrace{\vec{x}'}_{X'}$ angezeigt.
Zur Orientierung
Ziel ist es, Koordinatengleichungen für die Abbildung $\alpha$ herzuleiten. Wenn du fit bist, dann probiere es eigenständig und kontrolliere deine Ergebnisse im Applet unten. Im nächsten Abschnitt gibt es bei Bedarf Hilfestellungen.
Quellen
- [1]: Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen corporen - Urheber: Albrecht Dürer - Lizenz: Gemeinfrei