Problemstellung
Zur Orientierung
Es ist gar nicht so einfach, einen 3D-Weltausschnitt so auf einer 2D-Fläche abzubilden, dass räumliche Strukturen adäquat erfasst werden. Das zeigt z.B. die Darstellung aus einem antiken Grab, bei der die räumliche Wahrnehmung – beabsichtigt oder auch nicht beabsichtigt – nicht ganz gelungen ist.
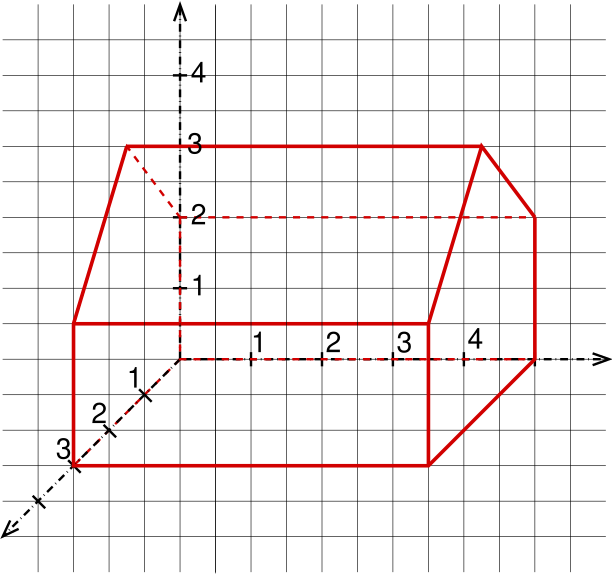
Wie man das besser machen kann hast du bereits gelernt. Bei einfach geformten 3D-Objekten besteht ein gängiger Ansatz darin, ein Schrägbild dieses Objekts zu konstruieren. Die Abbildung verdeutlicht diesen Ansatz.
Unser Ziel hier besteht darin, die Konstruktion von Schrägbildern mit Hilfe geeigneter geometrischer Abbildungen zu beschreiben.
Das Problem präzisieren
Erkunde das zu bearbeitende Problem anhand des folgenden Applets. Bearbeite hierzu die darunter aufgeführten Aufgaben.
Zum Herunterladen: projektion_schraegbild_quader.ggb
Aufgabe 1
Betrachte zunächst die Ausgangssituatuion.
Gegeben
- Gegeben ist eine 3D-Miniwelt. Wir betrachten einfache Welten, die aus Punkten und Kanten bestehen.
Im Applet ist ein Quader als 3D-Minwelt bereits vorgegeben. Im Applet kann man im unteren Fenster die betrachtete 3D-Minwelt verändern und selbst konfigurieren. Hierzu muss man nur die betrachteten Punkte und Kanten in den entsprechenden Eingabefeldern eintragen. Probiere das selbst aus. Ändere die 3D-Miniwelt so ab, dass das Haus in der Abbildung oben erscheint.
Aufgabe 2
Betrachte auch die gewünschte Zielsituatuion.
Gesucht
- Gesucht ist ein Verfahren zur Erzeugung von Schrägbildern.
Mit dem Verfahren soll zu einem beliebigen Ausgangspunkt $X$ der zugehörige Bildpunkt $X'$ berechnet werden. Im Applet kannst du im 3D-Grafikfenster den Punkt $X$ im vorgegebenen 3D-Objekt zu verschiedenen Eckpunkten bewegen. Probiere das selbst aus. Im Schrägbild im 2D-Grafikfenster bewegt sich $X'$ an die entsprechende Bildposition. Angezeigt wird auch die jeweilige Zuordnung $\alpha: \underbrace{\vec{x}}_{X} \rightarrow \underbrace{\vec{x}'}_{X'}$.
Zur Orientierung
Ziel ist es, eine Vektorgleichung für die Abbildung $\alpha$ herzuleiten. Wenn du fit bist, dann probiere es eigenständig und kontrolliere deine Ergebnisse im Applet unten. Im nächsten Abschnitt gibt es bei Bedarf Hilfestellungen.
Quellen
- [1]: Darstellung aus dem Grab des Sebekhotep - Urheber: Metropolitan Museum of Art - Lizenz: Gemeinfrei
- [2]: Schrägbild eines Hauses - Urheber: Ag2gaeh - Lizenz: Creative Commons BY-SA 4.0