Anwendung - Wege im Gitternetz

Das Problem

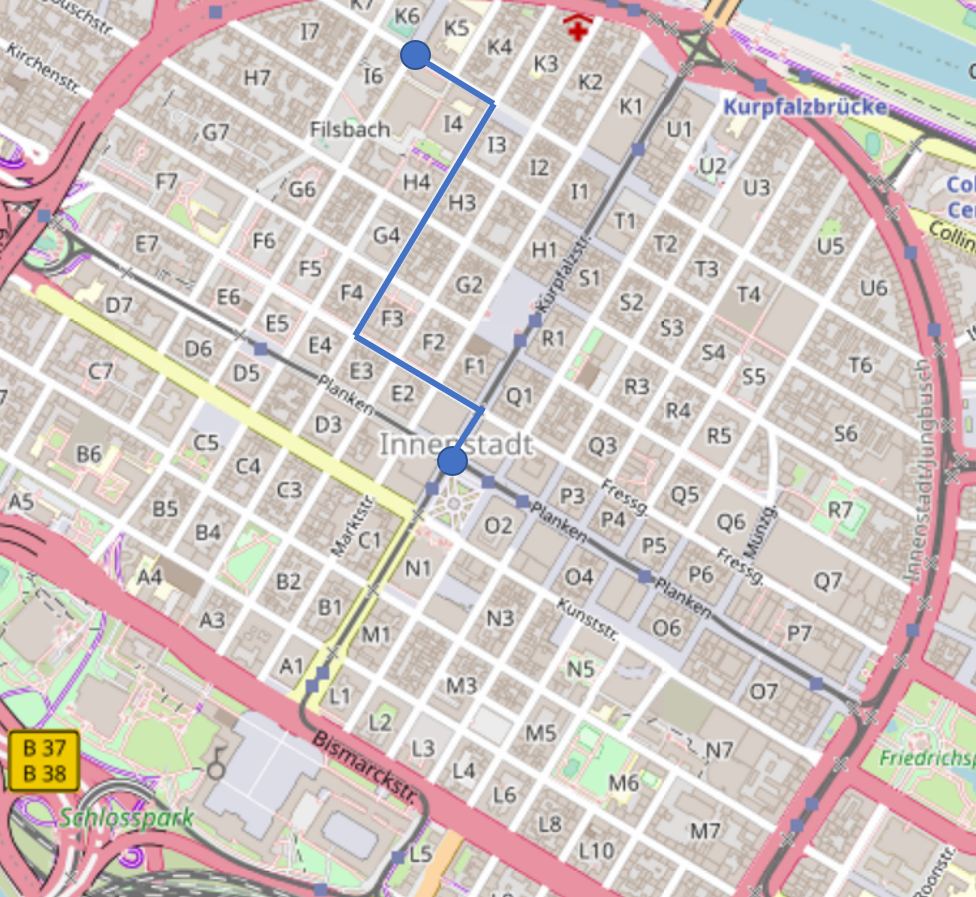
Du willst in der Mannheimer Innenstadt vom Johannes-Kepler-Gymnasium zum Paradeplatz laufen. Wie viele verschiedene (kürzeste) Wege sind hier möglich?
Die Karte der Mannheimer Innenstadt verdeutlicht die Situation. [1].

Wege auswählen

Betrachte die etwas vereinfachte Situation, die im Applet dargestellt ist.

Anleitung für das Applet

• Im oberen Auswahlblock kannst du die Felder anklicken und somit eine Auswahl an roten Feldern erzeugen.
• Den hervorgehobenen blauen Punkt kannst du unten im Gitternetz bewegen.

Zum Herunterladen: wegeimgitternetz1.ggb

Aufgabe 1

(a)Markiere mit dem bewegbaren Punkt einen Punkt im Gitternetz.

(b)Erzeuge mit geeigneten Auswahlen unterschiedliche Wege zum Punkt im Gitternetz.

(c)Erläutere, wie der angezeigte Weg im Gitternetz mit der eingestellten Auswahl zusammenhängt.

Anzahl der Wege bestimmen

Jetzt geht es darum, die Anzahl der Wege vom Startpunkt ganz oben bis zum voreingestellten Punkt im Gitternetz zu bestimmen.

Anleitung für das Applet

• Im oberen Auswahlblock kannst du die Felder anklicken und somit eine Auswahl an roten Feldern erzeugen.
• Den hervorgehobenen blauen Punkt kannst du unten im Gitternetz bewegen.
• Mit den Kontrollkästchen kannst du Anzahlen einblenden. Nutze diese Kästchen nur zur Kontrolle.

Zum Herunterladen: wegeimgitternetz2.ggb

Aufgabe 2

Im Gitternetz ist bereits ein Punkt vorgegeben. Wie viele verschiedene (kürzeste) Wege gibt es im Gitternetz zu diesem Punkt?

(a) Bestimme diese Anzahl zunächst experimentell, indem du alle möglichen Wege mit geeigneten Auswahlen erzeugst.
Um den Überblick zu behalten, kannst du die Auswahlen so dokumentieren:

RLLLR, ...

Kontrolliere die ermittelte Anzahl, indem du die Zahldarstellung einblendest.

(b) Beschreibe die Anzahl der Wege mit einem Binomialkoeffizienten. Kontrolliere die Beschreibung, indem du die Textdarstellung einblendest.

Eigenschaften des Binomialkoeffizienten verdeutlichen

Mit Hilfe der Gitternetzdarstellung lassen sich einige Eigenschaften des Binomialkoeffizienten gut verdeutlichen.

Aufgabe 3

Begründe die folgenden Zusammenhänge anhand des Gitternetzes:

$\begin{pmatrix} 8 \\ 3 \end{pmatrix} = \begin{pmatrix} 8 \\ 5 \end{pmatrix}$

$\begin{pmatrix} 6 \\ 4 \end{pmatrix} = \begin{pmatrix} 6 \\ 2 \end{pmatrix}$

$\begin{pmatrix} n \\ k \end{pmatrix} = \begin{pmatrix} n \\ n-k \end{pmatrix}$

Aufgabe 4

Erläutere die folgenden Regeln am Gitternetz:

$\begin{pmatrix} n \\ 0 \end{pmatrix} = 1$

$\begin{pmatrix} n \\ n \end{pmatrix} = 1$

Aufgabe 5

Begründe die folgenden Zusammenhänge anhand des Gitternetzes:

$\begin{pmatrix} 5 \\ 3 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} + \begin{pmatrix} 4 \\ 3 \end{pmatrix}$

$\begin{pmatrix} 8 \\ 4 \end{pmatrix} = \begin{pmatrix} 7 \\ 3 \end{pmatrix} + \begin{pmatrix} 7 \\ 4 \end{pmatrix}$

$\begin{pmatrix} n+1 \\ k+1 \end{pmatrix} = \begin{pmatrix} n \\ k \end{pmatrix} + \begin{pmatrix} n \\ k+1 \end{pmatrix}$