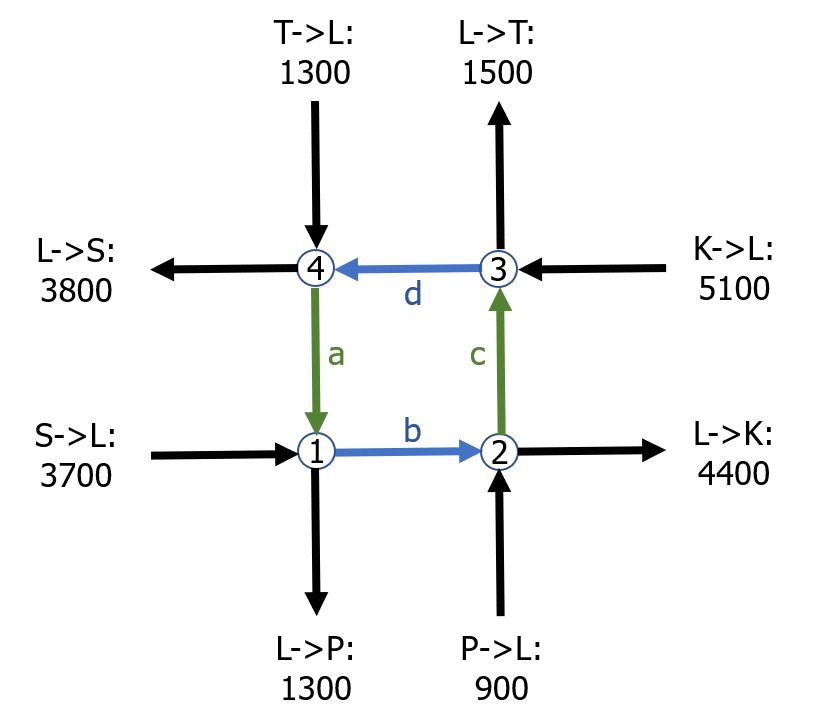
Ergebnisse deuten

Die im Modell erzielten Ergebnisse im Kontext deuten

Wir sind von folgenden Modellannahmen ausgegangen.

Anschließend haben wir das zugehörige lineare Gleichungssystem gelöst.

$\begin{array}{lrcr}[1]& 3700+a& =& 1300+b\\ [2]& 900+b& =& 4400+c\\ [3]& 5100+c& =& 1500+d\\ [4]& 1300+d& =& 3800+a\end{array}$

Das LGS hat unendlich viele Lösungen. Wir können die Lösungen mit einer beliebigen reellen Zahl $t$ so beschreiben:

• $a=t+1100$
• $b=t+3500$
• $c=t$
• $d=t+3600$

Aufgabe 1

Kann man tatsächlich jede reelle Zahl als sinnvolle Lösung im Kontext ansehen? Beurteile z.B. die Wahl $t=-100$. Begründe, dass $t$ folgende Bedingung erfüllen muss:

$t\ge 0$

Aufgabe 2

(a) Begründe, warum $t=1000000$ nicht möglich ist.

(b) Begründe, dass die folgende Bedingung immer erfüllt sein muss:

$a+b+c+d\le 11000$

Was würde es in der Realität bedeuten, wenn $a+b+c+d=11000$ gelten würde? erläutere kurz.

(c) Setze die oben aufgeführten Ergebnisse für $a$, $b$, $c$, $d$ in die Ungleichung $a+b+c+d\le 11000$ ein und folgere hieraus, dass auch diese Bedingung für $t$ gelten muss:

$t\le 700$

Aufgabe 3

Mit welchem maximalen LKW-Verkehrsaufkommen muss man am Autobahnkreuz Landstuhl-West in den Abschnitten $a$, $b$, $c$ und $d$ rechnen, wenn man die oben angegebenen (gerundeten) Messwerte zu Grunde legt? Bestimme abschließend diese Werte.