Strukturierung – Lagebeziehungen bei Geraden
Ein Wissenspeicher
Da hier die Ergebnisse der vorherigen Abschnitte aus mathematischer Sicht präzisiert werden, ist es sehr wichtig, dass du dir alles Wichtige strukturiert aufschreibst. Du kannst dafür diesen Wissensspeicher benutzen.
Im Wissensspeicher soll übersichtlich und prägnant das neu Gelernte dokumentiert werden. Die vorgegebene Struktur auf dem Wissensspeicher soll sicherstellen, dass alles Wichtige festgehalten wird; so werden z.B. nicht nur Definitionen, sondern in der Regel auch Beispiele, Vernetzungen oder Konventionen gefordert. Der Wissensspeicher kann verwendet werden, um ein im Unterricht erstelltes Tafelbild einfacher ins Heft zu übertragen. Es ist mit ihm aber auch möglich, die Sicherung stärker schüler:innen-orientiert zu gestalten: Je nach Unterrichtsgestaltung können die Schüler:innen nach einer Erarbeitung und Besprechung den gesamten Wissensspeicher selbst ausfüllen (im Unterricht, ggf. auch in der Hausaufgabe) oder hierfür zusätzlich dieses Online-Schulbuch zu Hilfe nehmen.
Gegenseitige Lage von Geraden im 3D-Raum
Das folgende Applet zeigt 4 Geraden, die unterschiedlich zueinander liegen.
Zum Herunterladen: geraden.ggb
Aufgabe 1
Nenne die vier möglichen Lagebeziehungen von Geraden mit ihren Fachbegriffen und beschreibe kurz, was das jeweils bedeutet. Ordne jeder möglichen Lagebeziehung ein Beispiel aus dem Applet oben zu. Im Wissensspeicher gibt es hierfür eine Tabelle.
Relevante Eigenschaften der Geraden
In der Erkundung haben wir verschiedene Argumente genutzt, um die Lagebeziehungen von Geraden zu untersuchen. Im Wesentlichen sind hier zwei Faktoren relevant:
- Haben die Geraden (mindestens) einen gemeinsamen Punkt?
- In welche Richtung verlaufen die Geraden?
Aufgabe 2
(a) Begründe, dass es nicht ausreicht, nur eine Schnittpunktbestimmung durchzuführen.
Welche möglichen Ergebnisse gibt es bei einer Schnittpunktbestimmung? Überlege dir für jedes Ergebnis: Welche Lagebeziehung ist dann möglich?
(b) Begründe, dass es nicht ausreicht, nur die Richtungsvektoren der Geraden auf lineare Abhängigkeit zu untersuchen.
Es gibt hier nur zwei Möglichkeiten: Entweder die Richtungsvektoren sind linear abhängig oder unabhängig. Überlege dir jeweils, weilche Lagebeziehungen dann möglich sind.
Aufgabe 3
Die Lagebeziehung zwischen den beiden Geraden hängt also aus der Kombination der beiden genannten Eigenschaften ab. Es gibt entsprechend vier mögliche Fälle. Trage die richtige Lagebeziehung in das jeweilige Tabellenfeld ein.
| Mindestens ein Schnittpunkt. | Kein Schnittpunkt. | |
| Richtungsvektoren linear abhängig | ||
| Richtungsvektoren linear unabhängig |
Ein cleveres Verfahren zur Bestimmung der Lagebeziehung
Wir können die Lagebeziehung zweier Geraden nun untersuchen, indem wir eine Schnittpunktbestimmung durchführen und die Richtungsvektoren auf lineare Abhängigkeit untersuchen. Das ist jedoch recht aufwändig. Wir werden nun ein schnelleres Verfahren entwickeln.
Aufgabe 4
Was geht einfacher – eine Schnittpunktbestimmung oder die Untersuchung auf lineare Abhängigkeit? Begründe.
Aufgabe 5
Weil die Schnittpunktbestimmung relativ aufwändig ist, untersuchen wir in der Regel zuerst die beiden Richtungsvektoren auf lineare Abhängigkeit.
(a) Wir nehmen an, die beiden Richtungsvektoren sind linear abhängig. Welche Lagebeziehungen sind nun möglich?
(b) Bei linear abhängigen Richtungsvektoren gibt es nur zwei Möglichkeiten für die Lagebeziehung. Um eine endgültige Entscheidung zu treffen, brauchen wir nun allerdings keine Schnittpunktberechnung. Es reicht aus, einfach zu überprüfen, ob der Stützpunkt der einen Geraden auf der anderen Geraden liegt. Begründe, warum das so ist und inwiefern das einen Vorteil darstellt.
(c) Sind die Richtungsvektoren linear unabhängig, ist die Sache nicht so einfach. Hier ist nun doch eine Schnittpunktberechnung erforderlich. Nenne die möglichen Lagebeziehungen bei linear unabhängigen Richtungsvektoren und begründe, warum es nun nicht ausreicht, zu überprüfen, ob der eine Stützpunkt auf der anderen Geraden liegt.
Aufgabe 6
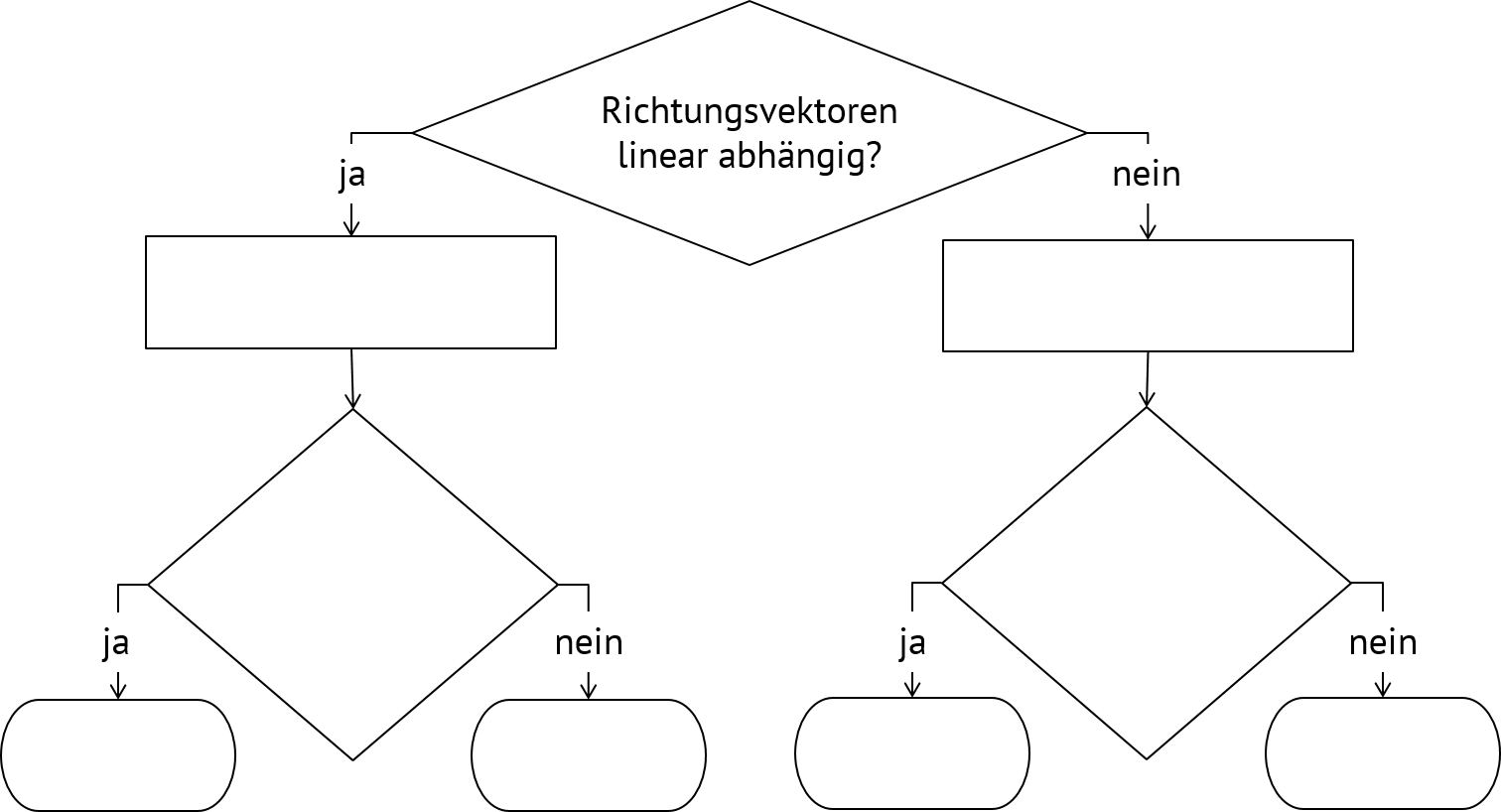
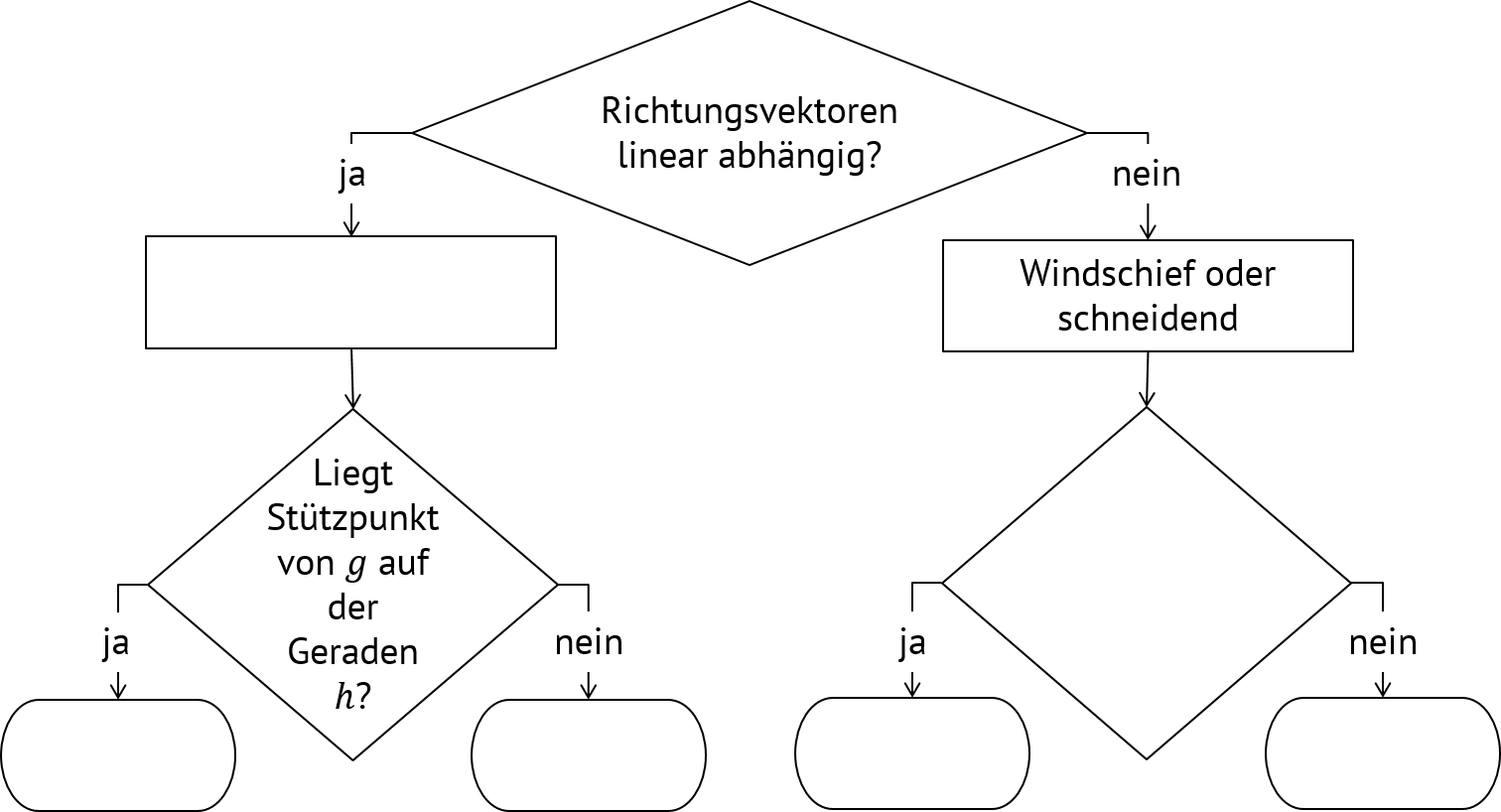
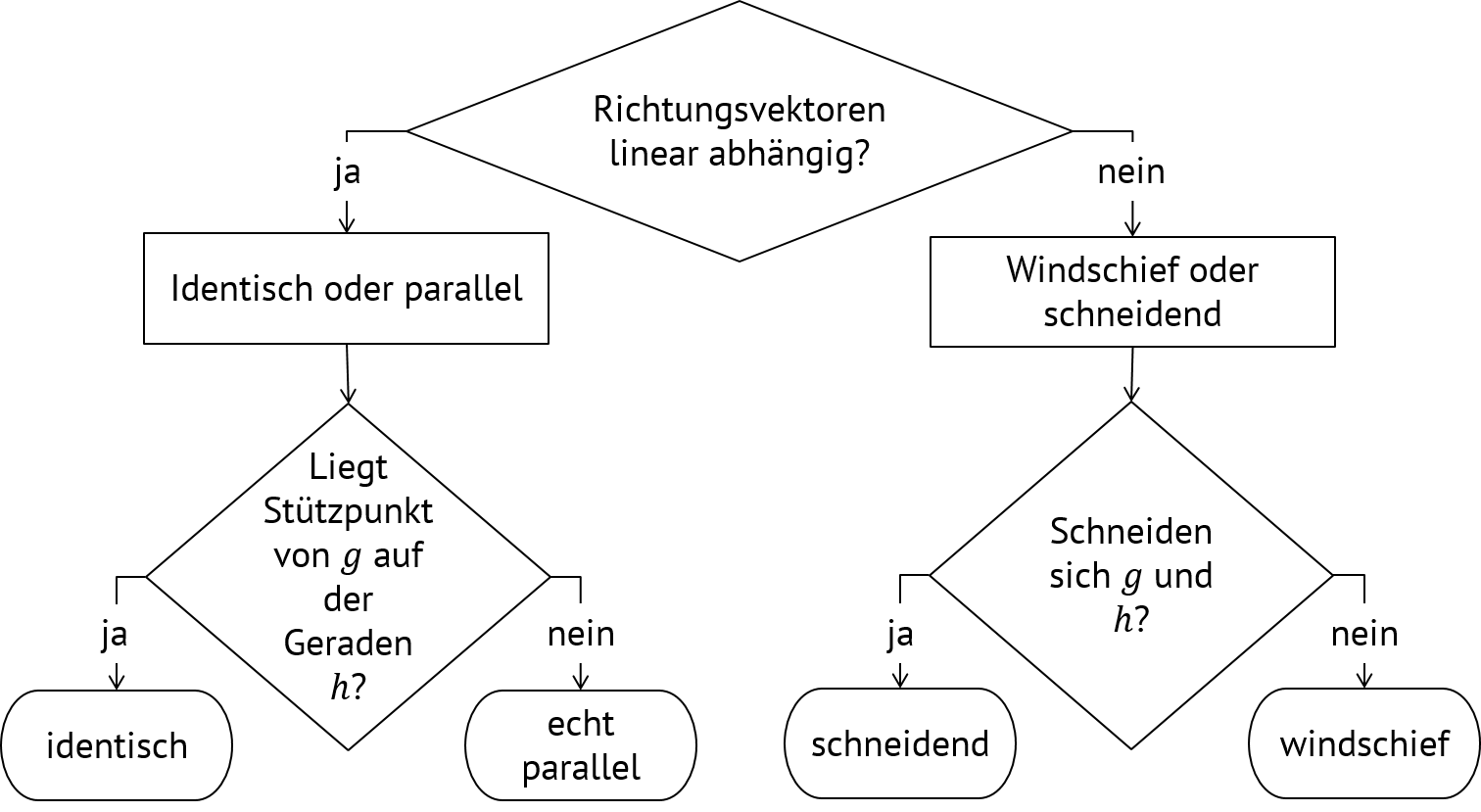
Mit den Ergebnissen der vorherigen Aufgabe können wir ein cleveres Verfahren zur Unteruschung der Lagebeziehungen formulieren. Dafür können wir dieses Formular füllen; du findest es auch im Wissensspeicher. Die Rauten stellen Fragestellungen dar; in die Rechtecke kommen vorläufige Lagebeziehungen, die zu dem Zeitpunkt des Verfahrens möglich sind. In die Figuren mit abgerundeten Ecken kommen die endgültigen Lagebeziehungen.
Bei dieser Darstellung handelt es sich um ein Flussdiagramm. Man nutzt solche Diagramme oft in der Informatik, um den Ablauf von Computerprogrammen darzustellen. Man kann damit aber auch ganz allgemein Algorithmen, also Handlungsvorschriften, darstellen.
In der Mathematik nutzt man an verschiedenen Stellen Algorithmen: Ein typisches Beispiel sind Konstruktionen in der Geometrie, zum Beispiel eine Achsenspiegelung. Auch die im vorherigen Abschnitt behandelte Schnittpunktbestimmung kann als ein kleiner Algorithmus aufgefasst werden. Aus anderen Themenfeldern lassen sich zum Beispiel Kurvendiskussionen (Analysis) und Signifikanztests (Stochastik) nennen.
Beispiele
Ein solches Verfahren trainiert man am besten, indem man es mehrfach bei einfachen Beispielen anwendet.
Aufgabe 7
Wende das Verfahren für jedes der nachfolgenden Beispiel an. Achte darauf, dass du ordentlich vorgehst. Dann kannst du deine Lösungen später als „Musterbeispiele“ verwenden.
Beispiel 1:
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ (mit $s \in \mathbb{R}$)
$j: \vec{x} = \left(\begin{array}{c} -4 \\ -3 \\ 2 \end{array}\right) + k \cdot \left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array}\right)$ (mit $k \in \mathbb{R}$)
Beispiel 2:
$g: \vec{x} = \left(\begin{array}{c} 2 \\ -5 \\ 2 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right)$ (mit $t \in \mathbb{R}$)
$i: \vec{x} = \left(\begin{array}{c} -2 \\ 4 \\ 4 \end{array}\right) + r \cdot \left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$ (mit $r \in \mathbb{R}$)
Beispiel 3:
$g: \vec{x} = \left(\begin{array}{c} 2 \\ -5 \\ 2 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right)$ (mit $t \in \mathbb{R}$)
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ (mit $s \in \mathbb{R}$)
Beispiel 4:
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ (mit $s \in \mathbb{R}$)
$i: \vec{x} = \left(\begin{array}{c} -2 \\ 4 \\ 4 \end{array}\right) + r \cdot \left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$ (mit $r \in \mathbb{R}$)
Quellen
- [1]: Leeres Flussdiagramm zur Untersuchung der Lagebeziehungen - Urheber: FR - Lizenz: inf-schule.de
- [2]: Teil-ausgefülltes Flussdiagramm zur Untersuchung der Lagebeziehungen - Urheber: FR - Lizenz: inf-schule.de
- [3]: Fertiges Flussdiagramm zur Untersuchung der Lagebeziehungen - Urheber: FR - Lizenz: inf-schule.de