Übungen - Spurpunkte

Aufgabe 1 - Geraden visualisieren

Bestimme die Spurpunkte der beiden folgenden Geraden und veranschauliche ihre Lage im 3D-Koordinatensystem.

$g: \vec{x} = \left(\begin{array}{c} 1 \\ 8 \\ -2 \end{array}\right) + t \cdot \left(\begin{array}{c} -2 \\ 4 \\ -2 \end{array}\right)$ (mit $t \in \mathbb{R}$)

$h: \vec{x} = \left(\begin{array}{c} 6 \\ 4 \\ 2 \end{array}\right) + t \cdot \left(\begin{array}{c} 2 \\ 1 \\ -2 \end{array}\right)$ (mit $t \in \mathbb{R}$)

Aufgabe 2 - Anzahl der Spurpunkte

(a) Die Gerade $g$ mit der unten angegebenen Geradengleichung hat nur $2$ Spurpunkte. Begründe, warum das so ist. Erläutere auch, wie man das an der entsprechenden Rechnung feststellt.

$g: \vec{x} = \left(\begin{array}{c} 1 \\ 0 \\ 3 \end{array}\right) + t \cdot \left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$ (mit $t \in \mathbb{R}$)

(b) Gib eine Geradengleichung an, die nur die Spurpunkte $S_{12}$ und $S_{13}$ hat. Erläutere die Wahl der Geradengleichung.

(c) Wie viele Spurpunkte hat die folgende Gerade? Erläutere, wie man das sofort sieht und wie man dann direkt den / die Spurpunkt(e) bestimmt.

$g: \vec{x} = \left(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}\right) + t \cdot \left(\begin{array}{c} 0 \\ -2 \\ 0 \end{array}\right)$ (mit $t \in \mathbb{R}$)

(d) Warum helfen Spurpunkte bei der folgenden Geraden nicht bei der Veranschaulichung der Lage? Begründe kurz.

$h: \vec{x} = \left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) + t \cdot \left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right)$ (mit $t \in \mathbb{R}$)

Aufgabe 3 - Anzahl der Spurpunkte

Mit dem folgenden Applet kannst du den Richtungsvektor $\vec{u}$ der Geraden $g$ verändern. Nutze hierzu die Schieberegler $u1$, $u2$ und $u3$.

Zum Herunterladen: spurpunkte5.ggb

Je nach Einstellung ergeben sich unterschiedlich viele Spurpunkte. Bestimme passende Einstellungen für alle Situationen, die in der Tabelle dargestellt sind. Dokumentiere die Ergebnisse.

Lage der Gerade	Spurpunkte
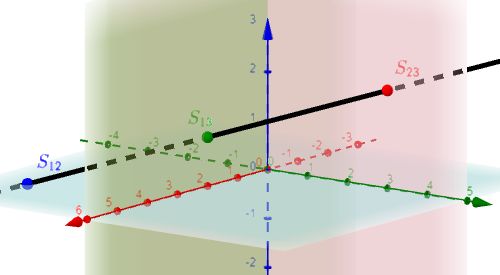	$g: \vec{x} = \left(\begin{array}{c} 1 \\ 1.5 \\ 1.5 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 1.5 \\ 0.5 \end{array}\right)$ $S_{12}(4|-3|0)$, $S_{13}(0|3|2)$, $S_{23}(2|0|1)$
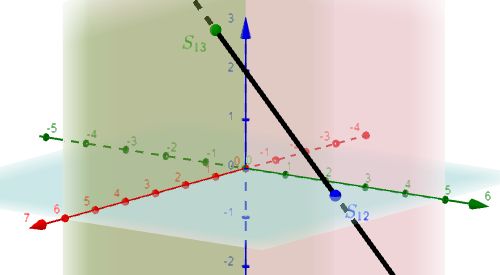	$S_{12}$, $S_{13}$ $g$ verläuft parallel zur $x_1$-$x_3$-Ebene
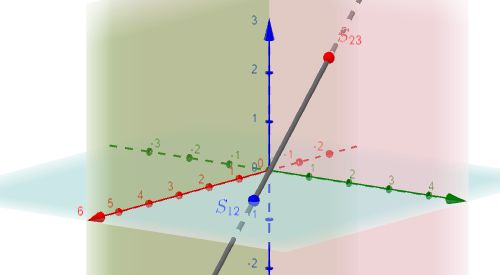	$S_{12}$, $S_{23}$
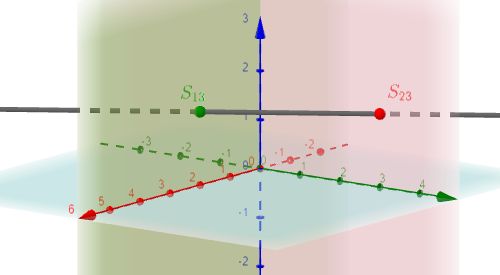	$S_{13}$, $S_{23}$
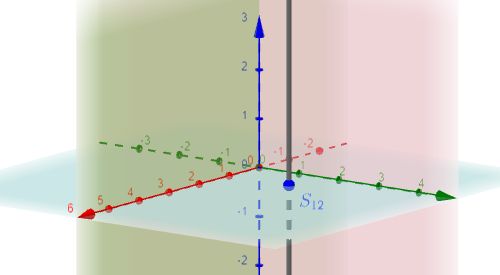	$S_{12}$
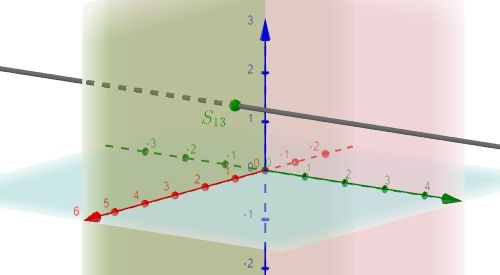	$S_{13}$
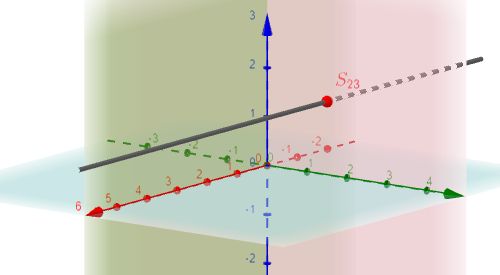	$S_{23}$