Erkundung - Beschleunigungsfunktion
Einstieg
Wir betrachten noch die Entwicklung eines 100m-Laufs.
Aufgabe 1
S. ist 100m-Läuferin. Sie möchte ihre Laufleistung weiter steigern. Sie ist daher sehr an Daten über die Entwicklung ihrer 100-Laufs interessiert. Erläutere: Beim 100m-Lauf interessiert man sich nicht nur für die Entwicklung der momentanen Geschwindigkeit, sondern auch die damit verbundene Entwicklung der momentanen Beschleunigung.
Erarbeitung
Die Tabelle zeigt (etwas überzeichnet) eine typische Entwicklung eines 100m-Laufs mit Hilfe von Funktionsgraphen.
| Zuordnung | Graph | Funktionen |
|---|---|---|
| Zeit -> Weg | 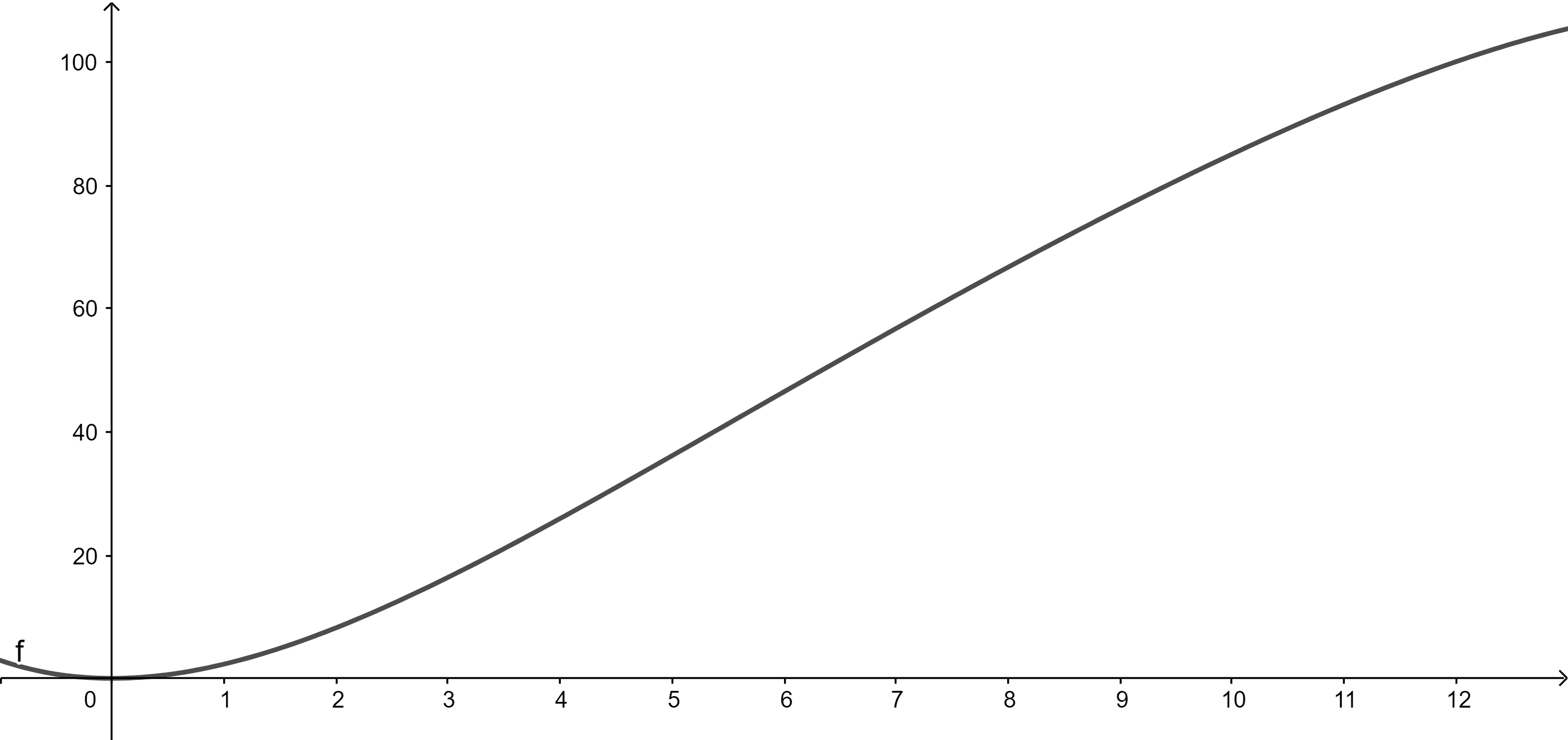 | |
| Zeit -> Geschwindigkeit | 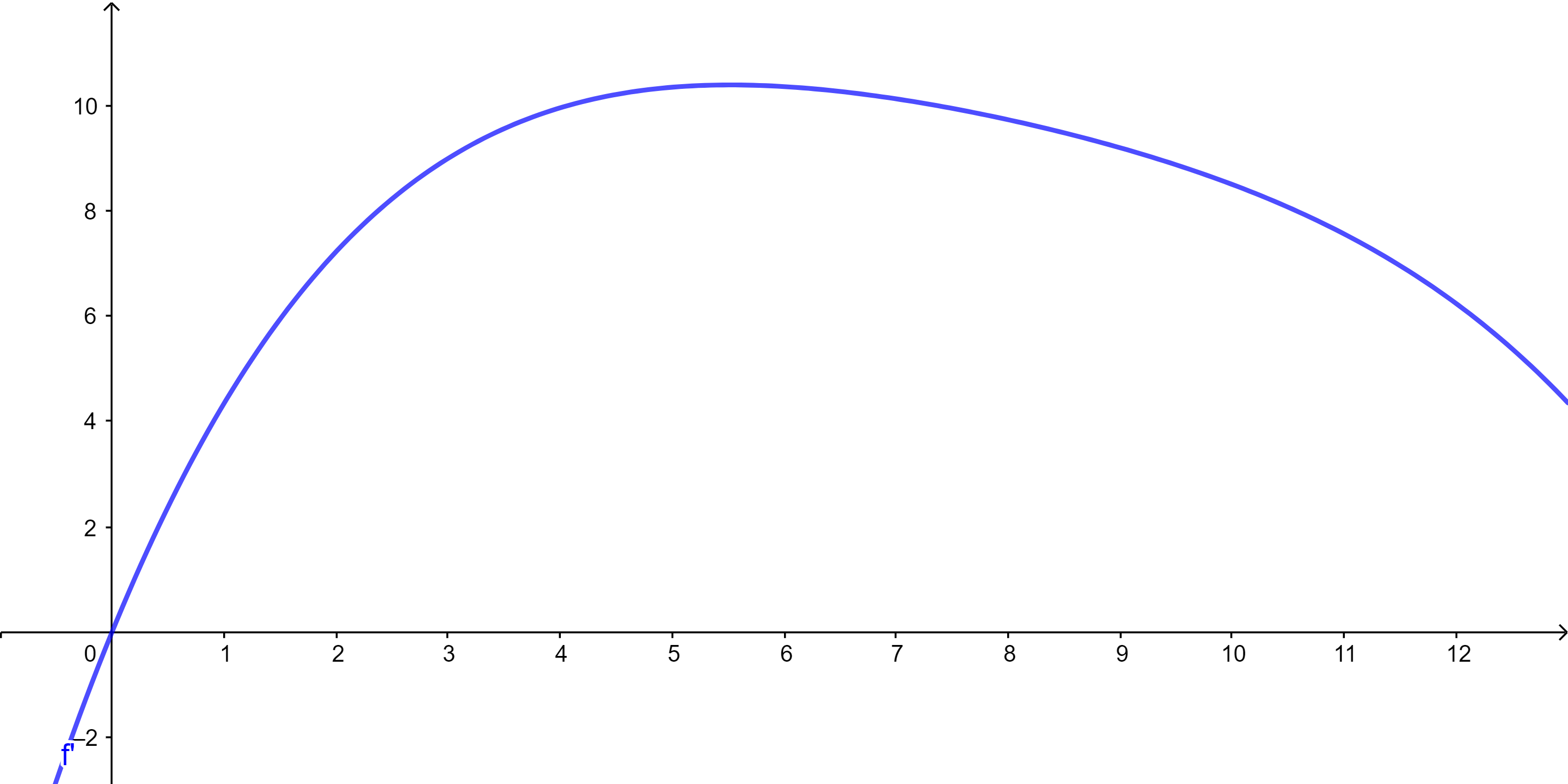 | |
| Zeit -> Beschleunigung | 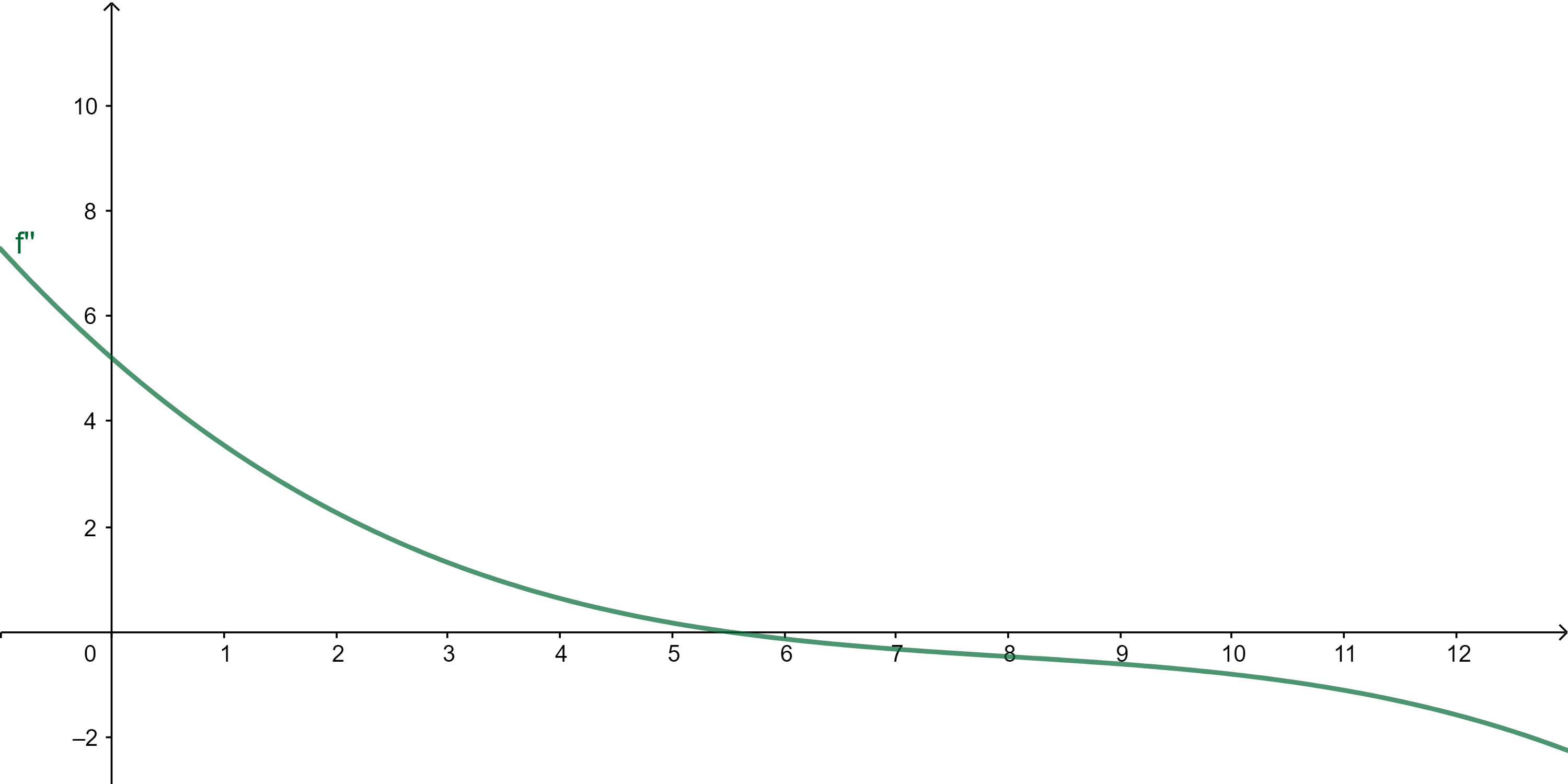 |
Aufgabe 2
Analysiere den Funktionsgraph zur Zeit-Weg-Funktion und kläre folgende Fragen.
- Wie lang hat der 100m-Lauf gedauert?
- Woran erkennt man (wenn man genau hinschaut), dass die Läuferin / der Läufer am Ende des Laufs etwas langsamer wird?
Aufgabe 3
Analysiere den Funktionsgraph zur Zeit-Geschwindigkeit-Funktion und kläre folgende Fragen.
- Welche maximale Geschwindigkeit hat die Läuferin / der Läufer erreicht (in m/s)?
- Wann wurde diese maximale Geschwindigkeit erreicht?
Aufgabe 4
Analysiere den Funktionsgraph zur Zeit-Beschleunigung-Funktion und kläre folgende Fragen.
- Wie zeigt sich die Zu- und Abnahme der momentanen Geschwindigkeit am Graph der Zeit-Beschleunigung-Funktion?
- Wie kann man am Graph der Zeit-Beschleunigung-Funktion erkennen, wann die maximale Geschwindigkeit erreicht wurde?
Aufgabe 5
Mit Geschwindigkeit beschreibt man die Änderung des zurückgelegten Wegs pro Zeit. Mit Beschleunigung beschreibt man die Änderung der Geschwindigkeit pro Zeit.
(a) Benutze diese Zusammenhänge, um folgende Zusammenhänge zwischen den Funktionen
(b) In der Tabelle oben findet man den Eintrag
Vertiefung
Aufgabe 5
Im Applet ist eine Zuordnungsvorschrift für die Funktion Zeit-Weg-Funktion
Zum Herunterladen: 100m_lauf2.ggb
Quellen
- [1]: 100m Lauf - Urheber: Stefan Brending - Lizenz: Creative Commons BY-SA 3.0


