Strukturierung - Hauptsatz der Differential- und Integralrechnung
Einen Zusammenhang zwischen Randfunktion und Integralfunktion herstellen
Die Integralfunktion $I_a$ entsteht aus einer vorgegebenen Randfunktion $f$ und einer unteren Grenze $a$ durch Integralberechnungen (d.h. geometrisch mit Hilfe orientierter Flächeninhalte bzw. analytisch mit Hilfe von Grenzwerten von Produktsummen).
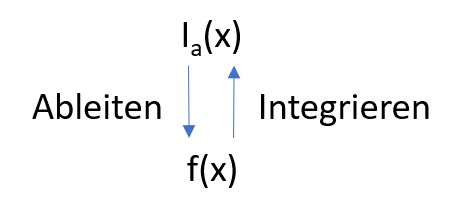
In den vorangehenden Abschnitten wurde auf unterschiedliche Weisen verdeutlicht, dass es zwischen einer Randfunktion $f$ und den zugehörigen Integralfunktionen $I_a$ einen fundamentalen Zusammenhang gibt: Wenn man die Integralfunktionen $I_a$ ableitet, dann erhält man die ursprüngliche Randfunktion $f$.
Das Applet verdeutlicht diesen Zusammenhang anhand eines Beispiels.
Zum Herunterladen: integrieren6.ggb
Aufgabe 1
Ergänze die Tabelle zur Verdeutlichung des Zusammenhangs zwischen Randfunktion und zugehörigen Integralfunktionen. Benutze das Applet, um die jeweiligen Integralfunktionen zu ermitteln. Achte darauf, auch den Wert für $a$ richtig einzustellen.
| $f(x)$ | $I_a(x)$ | $I_a'(x)$ |
|---|---|---|
| $f(x) = \frac{1}{10}x^3 - \frac{9}{10}x^2 + \frac{9}{5}x$ | $I_0(x) = \frac{1}{40}x^4 - \frac{3}{10}x^3 + \frac{9}{10}x^2$ | $I_0'(x) = ...$ |
| $f(x) = 2 - x$ | $I_0(x) = ...$ | $I_0'(x) = ...$ |
| $f(x) = 2 - x$ | $I_1(x) = ...$ | $I_1'(x) = ...$ |
| $f(x) = -\frac{1}{4}x^2 + x$ | $I_0(x) = ...$ | $I_0'(x) = ...$ |
| $f(x) = -\frac{1}{4}x^2 + x + 1$ | $I_3(x) = ...$ | $I_3'(x) = ...$ |
Den Zusammenhang zwischen Randfunktion und Integralfunktion präzise formulieren
Der Zusammenhang zwischen Randfunktion und zugehörigen Integralfunktionen stellt eine Verbindung her zwischen Integrieren (als zentrale Operation der Integralrechnung) und Ableiten bzw. Differenzieren (als zentrale Operation der Differentialrechnung). Er bildet den inhaltlichen Kern eines fundamentalen Satzes, den man Hauptsatz der Differential- und Integralrechnung nennt:
Hauptsatz der Differential- und Integralrechnung:
Betrachte die Ausgangssituation, dass eine Randfunktion $f$ und eine Zahl $a$ aus der Definitionsmenge von $f$ gegeben ist. Wenn die Randfunktion keine Sprungstellen hat (man sagt auch: wenn sie stetig ist), dann gilt:
$I_a'(x) = f(x)$
Die Ableitung einer Integralfunktion $I_a$ zur Randfunktion $f$ ergibt die ursprüngliche Randfunktion $f$.
Aufgabe 2
Im Hauptsatz wird eine Voraussetzung an die Randfunktion formuliert: Die Randfunktion $f$ darf keine Sprungstellen haben. Verdeutliche anhand des folgenden Applets: Wenn die Randfunktion eine Sprungstelle hat, dann entsteht an dieser Stelle bei der Integralfunktion eine Knickstelle. Die Integralfunktion hat an dieser Stelle dann keine eindeutig bestimmbare Steigung bzw. es existiert an dieser Stelle keine Ableitung. An solchen Stellen kann man daher den oben formulierten Zusammenhang nicht herstellen.
Zum Herunterladen: integrieren5.ggb

