Übungen – Satz von Bayes
Aufgabe 1 – Satz von Bayes
(a) Im unteren Applet sind die Vorher-Wahrscheinlichkeiten bereits eingetragen. Bestimme mit diesen gegebenen Wahrscheinlichkeiten die Nachher-Wahrscheinlichkeiten. Kontrolliere die Ergebnisse erst, nachdem du alle Berechnungen durchgeführt hast.
(b) Wenn du auf die gelb/orange unterlegten Felder klickst, dann werden die betreffenden Wahrscheinlichkeiten im Einheitsquadrat veranschaulicht. Die jeweilige Wahrscheinlichkeit wird immer durch den Anteil von „rot“ an „rot+gelb“ dargestellt. Erkläre anhand dieser Darstellung den Unterschied zwischen den Vorher- und Nachher-Wahrscheinlichkeiten.
Zum Herunterladen: vorhernachher2.ggb
Aufgabe 2 – Würfel werfen / Version 1
Zwei Würfel – ein Standardwürfel (SW) und ein Pyramidenwürfel (PW) – liegen bereit.

Die Wahrscheinlichkeitsverteilungen der beiden Würfel sind bekannt:
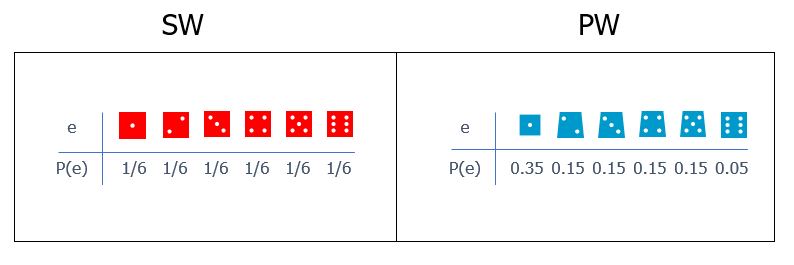
Betrachte folgende Situation: Es wird zufällig ein Würfel ausgewählt. Du weißt nicht, welcher Würfel gewählt wurde. Jetzt wird der gewählte Würfel geworfen. Du erfährst nur das Ergebnis des Würfelwurfs – eine $1$.
Benutze für die weitere Arbeit folgende Bezeichnungen:
- $B$: Der zufällig gewählte Würfel ist der PW.
- $\overlinepatch{B}$: Der zufällig gewählte Würfel ist der SW.
- $A$: Beim Werfen des gewählten Würfels fällt eine $1$.
- $\overlinepatch{A}$: Beim Werfen des gewählten Würfels fällt keine $1$.
Beschreibe und bestimme die Wahrscheinlichkeiten in der folgenden Tabelle:
| Schreibweise | Deutung | Wert |
|---|---|---|
| $P(B)$ | Wahrscheinlichkeit, dass der zufällig gewählte Würfel ein PW ist. | $P(B) = 0.5$ |
| $P(\overlinepatch{B})$ | Wahrscheinlichkeit, dass ... | $P(\overlinepatch{B}) = ...$ |
| $P(A|B)$ | Wahrscheinlichkeit, dass beim Werfen des gewählten Würfels eine $1$ fällt, wenn der gewählte Würfel der ... ist. | $P(A|B) = 0.35 = \frac{7}{20}$ |
| $P(\overlinepatch{A}|B)$ | Wahrscheinlichkeit, dass ... | $P(\overlinepatch{A}|B) = ...$ |
| $P(A|\overlinepatch{B})$ | Wahrscheinlichkeit, dass ... | $P(A|\overlinepatch{B}) = ...$ |
| $P(\overlinepatch{A}|\overlinepatch{B})$ | Wahrscheinlichkeit, dass ... | $P(\overlinepatch{A}|\overlinepatch{B}) = ...$ |
| $P(A)$ | Wahrscheinlichkeit, dass der zufällig gewählte Würfel beim Werfen eine $1$ liefert. | $P(A) = ...$ |
| $P(\overlinepatch{A})$ | Wahrscheinlichkeit, dass ... | $P(\overlinepatch{A}) = ...$ |
| $P(B|A)$ | Wahrscheinlichkeit, dass der gewählte Würfel der ... ist, wenn beim Werfen des Würfels ... | $P(B|A) = ...$ |
| $P(\overlinepatch{B}|A)$ | Wahrscheinlichkeit, dass ... | $P(\overlinepatch{B}|A) = ...$ |
| $P(B|\overlinepatch{A})$ | Wahrscheinlichkeit, dass ... | $P(B|\overlinepatch{A}) = ...$ |
| $P(\overlinepatch{B}|\overlinepatch{A})$ | Wahrscheinlichkeit, dass ... | $P(\overlinepatch{B}|\overlinepatch{A}) = ...$ |
Zur Kontrolle kannst du das Applet aus Aufgabe 1 benutzen (mit den passend eingegebenen Vorher-Wahrscheinlichkeiten).
Aufgabe 3 – Würfel werfen / Version 2
Zwei Würfel – ein Standardwürfel (SW) und ein Pyramidenwürfel (PW) – liegen bereit.

Die Wahrscheinlichkeitsverteilungen der beiden Würfel sind bekannt:

Betrachte folgende Situation: Es wird zufällig ein Würfel ausgewählt. Du weißt nicht, welcher Würfel das ist. Jetzt wird der gewählte Würfel geworfen. Du erfährst nur das Ergebnis des Würfelwurfs.
Wir betrachten jetzt nicht nur zwei mögliche Indiz-Ereignisse. Im vorliegenden Kontext ist es sinnvoll, alle möglichen Augenzahlen separat zu betrachten.
Benutze für die weitere Arbeit folgende Bezeichnungen:
- $B$: Der zufällig gewählte Würfel ist der PW.
- $\overlinepatch{B}$: Der zufällig gewählte Würfel ist der SW.
- $A_1$: Beim Werfen des gewählten Würfels fällt eine $1$.
- $A_2$: Beim Werfen des gewählten Würfels fällt eine $2$.
- $A_3$: Beim Werfen des gewählten Würfels fällt eine $3$.
- $A_4$: Beim Werfen des gewählten Würfels fällt eine $4$.
- $A_5$: Beim Werfen des gewählten Würfels fällt eine $5$.
- $A_6$: Beim Werfen des gewählten Würfels fällt eine $6$.
(a) Beim Werfen des gewählten Würfels fällt die $2$. Bestimme die Nachher-Wahrscheinlichkeit $P(B|A_2)$.
(b) Beim Werfen des gewählten Würfels fällt die $6$. Bestimme die Nachher-Wahrscheinlichkeit $P(B|A_6)$.
(c) Gib die folgenden Nachher-Wahrscheinlichkeiten an. Musst du diese hier explizit ausrechnen? Begründe dein Vorgehen.
- Nachher-Wahrscheinlichkeit $P(B|A_3)$, wenn beim Werfen des gewählten Würfels die $3$ fällt.
- Nachher-Wahrscheinlichkeit $P(B|A_4)$, wenn beim Werfen des gewählten Würfels die $4$ fällt.
- Nachher-Wahrscheinlichkeit $P(B|A_5)$, wenn beim Werfen des gewählten Würfels die $5$ fällt.
(d) Beschreibe eine Strategie, um anhand der gefallenen Augenzahl den geworfenen Würfel zu bestimmen. Begründe die Strategie mit Hilfe deiner bisherigen Berechnungen.
Aufgabe 4 – Früherkennung von Krankheiten
Zur Früherkennung von Krankheiten werden Menschen ab einem bestimmten Alter aufgefordert, entsprechende Vorsorgeuntersuchungen durchführen zu lassen. Zur Früherkennung von Darmkrebs gibt es z. B. die Möglichkeit, mit einem Stuhltest zu untersuchen, ob sich Blut im Stuhl befindet. Dies ist dann ein Hinweis darauf, dass sich möglicherweise ein Karzinom gebildet hat.
Wir gehen hier von folgenden Daten aus:
- Der Stuhltest hat eine Sensitivität von 50 %.
- Der Stuhltest hat eine Spezifität von 97 %.
- Die Prävalenz in der betrachteten Altersgruppe beträgt 0.2%.
(a) Z. hat eine Stuhlprobe abgegeben und wird zur behandelnden Ärztin bestellt. Die Ärztin teilt Z. das Ergebnis mit: „Der Test war positiv.“ Z. ist total niedergeschlagen: „Bei einer Sensitivität von 50 % heißt das ja wohl, dass es mich mit einer 50:50 Wahrscheinlichkeit getroffen hat.“ Welchen Denkfehler hat Z. hier gemacht? Füge die Bausteine „erkrankt sein“ und „ein positives Testergebnis erhalten“ an die passenden Stellen ein.
Deutung der Sensitivität: Wahrscheinlichkeit dafür, dass ... unter der Bedingung, dass ...
Fehldeutung von Z: Wahrscheinlichkeit dafür, dass ... unter der Bedingung, dass ...
(b) Zur genaueren Einschätzung der Situation betrachten wir folgende Ereignisse:
- $B$: Die zufällig gewählte Person ist an Darmkrebs erkrankt.
- $\overlinepatch{B}$: Die zufällig gewählte Person ist nicht an Darmkrebs erkrankt.
- $A$: Der Stuhltest liefert ein positives Testresultat.
- $\overlinepatch{A}$: Der Stuhltest liefert ein negatives Testresultat.
Ordne den vorgegebenen Daten die passenden Wahrscheinlichkeiten zu. Zur Wahl stehen: $P(A) = ...$, $P(B) = ...$, $P(A|B) = ...$, $P(\overlinepatch{A}|\overlinepatch{B}) = ...$, $P(B|A) = ...$, $P(\overlinepatch{B}|\overlinepatch{A}) = ...$.
- Sensitivität von 50 %:
- Spezifität von 97 %:
- Prävalenz von 0.2 %:
(c) Hier sollst du die Situation anhand konkreter Zahlenwerte durchspielen. Betrachte eine Situation mit insgesamt 100000 Personen.
| $B$: Person hat Darmkrebs |
$\overlinepatch{B}$: Person hat kein Darmkrebs |
Gesamtanzahl der Personen |
|
|---|---|---|---|
| $A$: Test ist positiv |
... | ... | ... |
| $\overlinepatch{A}$: Test ist negativ |
... | ... | ... |
| Gesamtanzahl der Personen |
... | ... | 100000 |
Ergänze die Einträge in der Tabelle.
Z. interessiert sich insbesondere für folgende Zahl: Wie hoch ist der Anteil der erkrankten Personen an den Personen, die einen positiven Testbefund erhalten? Bestimme diesen Anteil.
(d) Benutze den Satz von Bayes, um die Wahrscheinlichkeit für eine Erkrankung an Darmkrebs unter der Bedingung, dass ein positiver Testbefund vorliegt, zu bestimmen. Vergleiche mit dem Ergebnis aus (c).
Zur Kontrolle: Verwende die Applets auf der vorherigen Seite.
Aufgabe 5 – Finanzwelt
In der Finanzwelt ist die Bewertung von Risiken und Unsicherheiten von entscheidender Bedeutung. Ziel ist es, aktuelle Informationen mit historischen Daten zu verknüpfen, um genauere Prognosen zu erstellen. Wir spielen dies hier mit fiktiven Daten zur Kapitalentwicklung durch.
Dabei betrachten wir folgende Ereignisse:
- $A_1$: der Zinssatz fällt
- $A_2$: der Zinssatz bleibt gleich
- $A_3$: der Zinssatz steigt
Wir gehen von einem unerfahrenen Kapitalanleger aus, der die Ereignisse naiv einschätzt:
Wahrscheinlichkeiten vorher:
- $P(A_1) = 0.2$: Die Wahrscheinlichkeit, dass der Zinssatz fällt, beträgt $0.2$.
- $P(A_2) = 0.5$: Die Wahrscheinlichkeit, dass der Zinssatz gleich bleibt, beträgt $0.5$.
- $P(A_3) = 0.3$: Die Wahrscheinlichkeit, dass der Zinssatz steigt, beträgt $0.3$.
Um die Kursentwicklung besser einschätzen zu können, wird ein Finanzberater hinzugezogen. Der Finanzberater behauptet, ...
- $B$: dass der Zinssatz steigt.
Bevor wir unser Kapital anlegen, besorgen wir uns Informationen über den Berater. Wir müssen ja wissen, wie zuverlässig sein Prognose ist:
- $P(B|A_1) = 0.1$: Die Wahrscheinlichkeit ...
- $P(B|A_2) = 0.2$: Die Wahrscheinlichkeit ...
- $P(B|A_3) = 0.7$: Die Wahrscheinlichkeit ...
Ziel ist es, die eingangs naiv gesetzten Wahrscheinlichkeiten mit Hilfe der Information über den Anlageberater neu zu bewerten.
Wahrscheinlichkeiten nachher:
- $P(A_1|B) = ?$: Die Wahrscheinlichkeit ...
- $P(A_2|B) = ?$: Die Wahrscheinlichkeit ...
- $P(A_3|B) = ?$: Die Wahrscheinlichkeit ...
(a) Ergänze jeweils die Deutung der oben aufgeführten bedingten Wahrscheinlichkeiten.
(b) Bestimme zunächst $P(B)$. Benutze hierzu die vorgegebenen Wahrscheinlichkeiten $P(B|A_1)$, $P(B|A_2)$ und $P(B|A_3)$.
(c) Bestimme anschließend die gesuchten Wahrscheinlichkeiten $P(A_1|B)$, $P(A_2|B)$ und $P(A_3|B)$.
(d) Deute die Ergebnisse. Beschreibe hierzu den Nutzen des Hinzuziehens eines Kapitalanlegers.

