Strukturierung - Veranschaulichung mit Spurpunkten
Eine Ebenengleichung in Koordinatenform geometrisch deuten
Je nachdem, wie intensiv du die vorangegangene Erkundung (vor allem Frage 3) bearbeitet hast, hast du die Ergebnisse dieser Seite schon herausgefunden. In diesem Fall ist der Mehrwert dieser Strukturierung, dass du dir noch einmal alle möglichen Fälle übersichtlich aufschreibst. Wenn du die Frage in der Erkundung nicht so ausführlich betrachtet hast, wirst du das auf dieser Seite nachholen.
Hier sollst du dir eine Übersicht darüber verschaffen, wie die Parameter
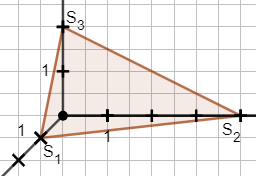
Wenn man die Lage einer Ebene im Koordinatensystem selbst skizzieren möchte, dann geht das am besten mit einem Ebenenausschnitt, der aus den Spurpunkten der Ebene gebildet wird. Das Applet macht Vorschläge, wie das aussehen könnte.
Zum Herunterladen: koordinatenform5.ggb
Aufgabe 1
Teste die Fälle, in denen es 3 Spurpunkte, 2 Spurpunkte oder nur 1 Spurpunkt gibt. Stelle jeweils geeignete Ebenengleichungen ein und wähle das passende Kontrollkästchen aus, um die Darstellung der Ebene anzuzeigen. Stelle die Ergebnisse in Tabellenform zusammen.
| Bedingung | Spurpunkte | Beispiel |
|---|---|---|
 | ||

