Zusammenfassung - Orthogonalität und Lagebeziehungen

Lagebeziehungen zwischen zwei Ebenen

Die Tabelle zeigt mögliche Lagebeziehungen von zwei Ebenen. Beachte, dass die Lagebeziehung "schneiden sich orthogonal" ein Spezialfall der Lagebeziehung "schneiden sich" ist.

Wir setzen voraus, dass die beiden Ebenen mit einer Ebengleichung in Normalenform gegeben sind. Also: $E_1: [\vec{x} - \vec{p_1}] \cdot \vec{n_1} = 0$ und $E_2: [\vec{x} - \vec{p_2}] \cdot \vec{n_2} = 0$.

Lagebeziehung	Veranschaulichung	Bedingung
die Ebenen schneiden sich		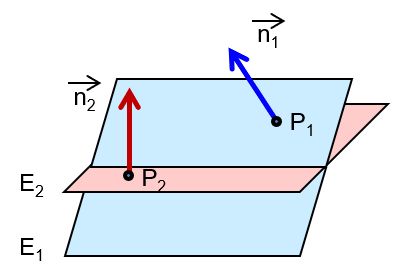$\vec{n_1}$ und $\vec{n_2}$ sind linear unabhängig
die Ebenen schneiden sich orthogonal		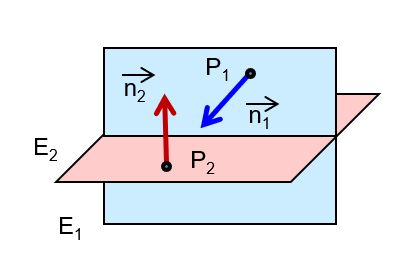$\vec{n_1}$ und $\vec{n_2}$ sind orthoginal
die Ebenen sind echt parallel		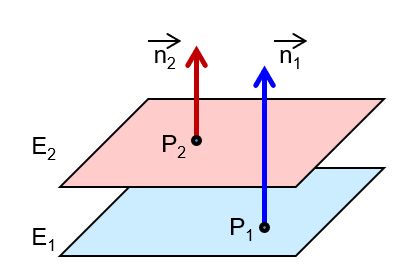$\vec{n_1}$ und $\vec{n_2}$ sind linear abhängig und $P_2$ liegt nicht in $E_1$ bzw. $P_1$ liegt nicht in $E_2$
die Ebenen sind identisch		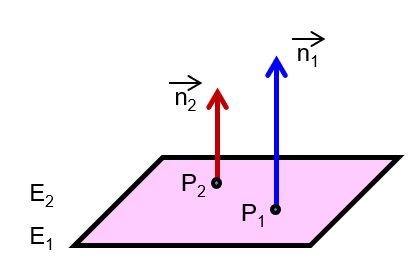$\vec{n_1}$ und $\vec{n_2}$ sind linear abhängig und $P_2$ liegt in $E_1$ bzw. $P_1$ liegt in $E_2$

Lagebeziehungen zwischen Geraden und Ebenen

Die Tabelle zeigt mögliche Lagebeziehungen von Geraden und Ebenen. Beachte, dass die Lagebeziehung "schneiden sich orthogonal" ein Spezialfall der Lagebeziehung "schneiden sich" ist.

Wir setzen voraus, dass die Gerade mit einer Geradengleichung in Parameterform und die Ebene mit einer Ebengleichung in Normalenform gegeben ist. Also: $g: \vec{x} = \vec{q} + r \cdot \vec{u}$ und $E: [\vec{x} - \vec{p}] \cdot \vec{n} = 0$.

Lagebeziehung	Veranschaulichung	Bedingung
die Gerade schneidet die Ebenen		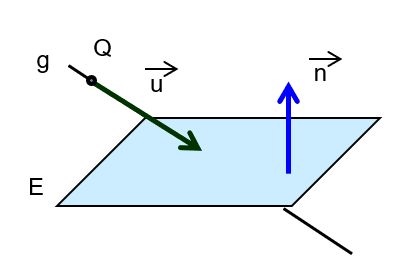$\vec{u}$ und $\vec{n}$ sind nicht orthogonal
die Gerade schneidet die Ebene orthogonal		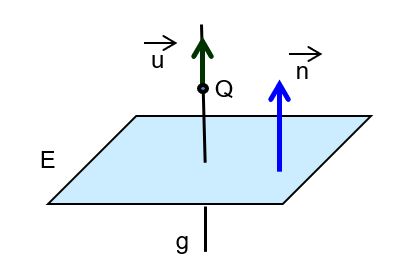$\vec{u}$ und $\vec{n}$ sind linear abhängig
die Gerade ist echt parallel zur Ebene		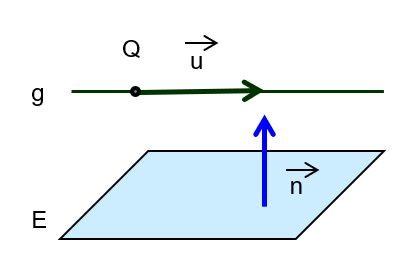$\vec{u}$ und $\vec{n}$ sind orthogonal und $Q$ liegt nicht in $E$
die Gerade liegt in der Ebene		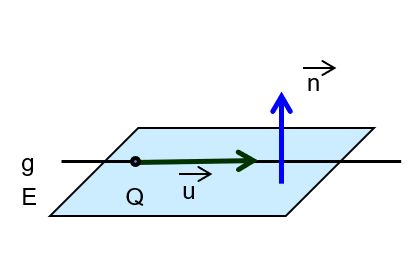$\vec{u}$ und $\vec{n}$ sind orthogonal und $Q$ liegt in $E$