Stabilisierung der Koffein-Folge

Das Grenzverhalten betrachten

Im letzten Abschnitt wurde die Koffein-Folge untersucht, die so festgelegt ist: $a_n$ beschreibt die Menge an Koffein [in mg] im Körper unmittelbar nach der $n$-te Tasse Kaffee (für $n = 1; 2; 3; ...$).

Die Folgenglieder $a_1; a_2; ...$ lassen sich mit einer rekursiven Darstellung berechnen:

$a_1 = 90$
$a_n = 0.5 \cdot a_{n-1} + 90$ für $n = 2; 3; ...$

Mit dem Applet kann man die Folgenglieder $a_1; a_2; ...$ (bis $a_{50}$) berechnen.

Zum Herunterladen: koffeinfolge_rekursiv.ggb

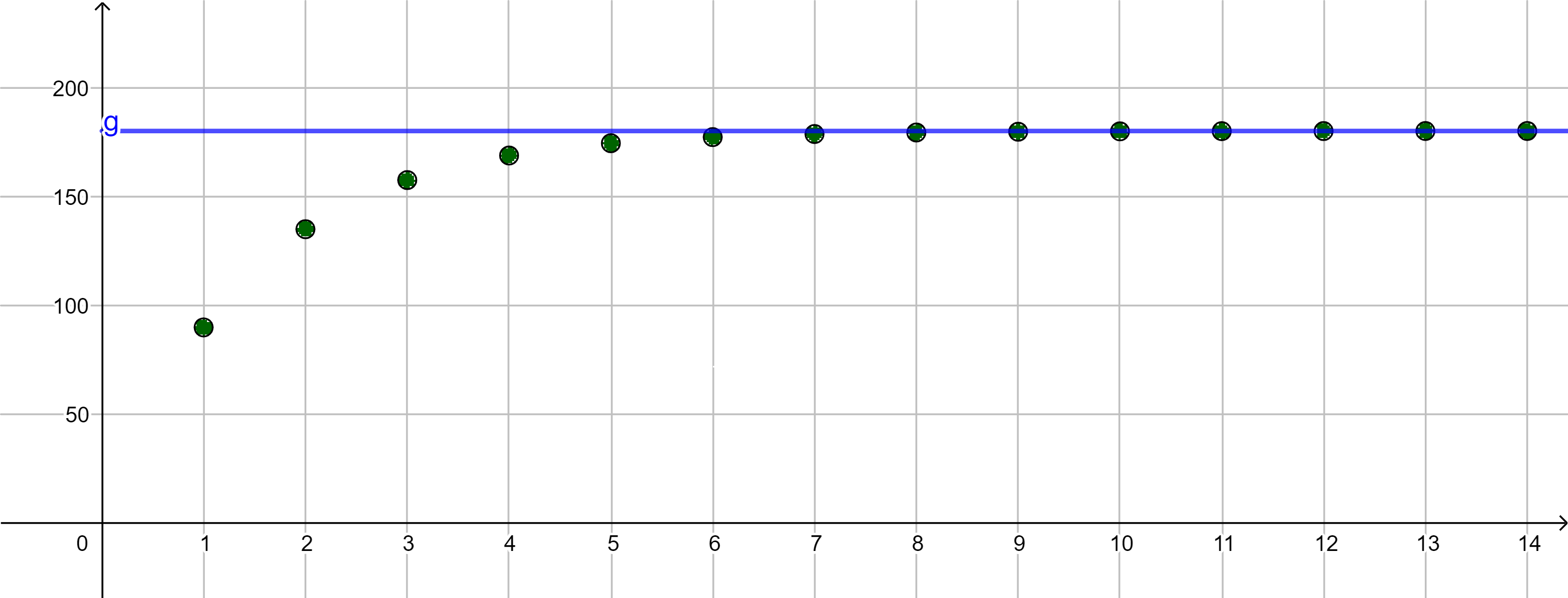
Die Folgenglieder stabilisieren sich beim Wert $180$. Der Graph der Folge verdeutlicht sehr gut das Stabilisierungsverhalten.

Das Grenzverhalten beschreiben

Die Folgenglieder der Koffein-Folge $\left( a_n \right)$ stabilisieren sich mit wachsender Platznummer bei einem Grenzwert $g = 180$.

Es gilt also $a_n \rightarrow 180$ für $n \rightarrow \infty$. Wir beschreiben diese Eigenschaft der Folge $\left( a_n \right)$ mit dieser Schreibweise:

$\lim\limits_{n \rightarrow \infty}{a_n} = 180$

Gelesen wird das so: "Der Limes (bzw. Grenzwert) von $a_n$ für $n$ gegen Unendlich ist gleich 180".

Wenn eine Folge sich bei einem Grenzwert stabilisiert, dann nennen wir sie konvergent, andernfalls divergent. Die Koffein-Folge $\left( a_n \right)$ ist also eine konvergente Folge, da sie den Grenzwert $g = 180$ hat. Man sagt auch: Die Folge konvergiert gegen den Grenzwert $g = 180$.

Das Ziel der folgenden Untersuchungen festlegen

Ziel der folgenden Abschnitte ist es, Stabilisierung bei Folgen weiter zu untersuchen.