Übungen - Grenzwerte
Aufgabe 1
Berechne jeweils so viele Folgenglieder, bis eine Stabilisierungstendenz erkennbar wird. Formuliere eine Konvergenzaussage.
| Beispiel | Folge $\left( a_n \right)$ | Folgenglieder | Grenzwertaussage |
|---|---|---|---|
| (a) | $a_n = 1 + \frac{1}{n}$ | $2; \frac{3}{2}; \frac{4}{3}; \frac{5}{4}; ...$ | $a_n \rightarrow 1$ bzw. $\lim\limits_{n \rightarrow \infty}{a_n} = 1$ |
| (b) | $a_n = - \frac{1}{n^2}$ | ||
| (c) | $a_n = 1.2^n$ | ||
| (d) | $a_n = (\frac{1}{10})^n$ | ||
| (e) | $a_n = \frac{n}{n+1}$ | ||
| (f) | $a_n = -n$ | ||
| (g) | $a_n = (-0.9)^n$ | ||
| (h) | $a_n = 2 - 0.5^n$ | ||
| (i) | $a_n = n^{0.5}$ | ||
| (j) | $a_n = (-1)^n \cdot \frac{1}{n}$ |
Aufgabe 2
Gib eine Folge $\left( a_n \right)$ an, die ...
- ... sich dem Grenzwert $1$ von unten nähert.
- ... sich dem Grenzwert $1$ von oben nähert.
- ... sich dem Grenzwert $1$ abwechseln von oben und unten nähert.
- ... sich dem Grenzwert $0$ sehr schnell von oben nähert.
- ... sich dem Grenzwert $0$ langsam von unten nähert.
Aufgabe 3
Hier wird ein Turm aus Würfeln gebaut. Der unterste Würfel hat die Kantenlänge 1 (m). Die Kantenlänge des jeweils nächsten Würfels beträgt das 0.9-fache des darunterliegenden Würfels. Die Folge $\left( a_n \right)$ beschreibt die Gesamthöhe eines Turms, der aus $n$ Würfeln besteht.

(a) Berechne die ersten Folgenglieder der Folge $\left( a_n \right)$ und stelle sie in einer Wertetabelle dar. Zur Kontrolle: $a_3 = 2,71$.
(b) Entwickle eine rekursive Berechnungsvorschrift für die Folge $\left( a_n \right)$.
(c) Hier eine explizite Berechnungsvorschrift für die Folge $\left( a_n \right)$:
$a_n = \displaystyle{\frac{1-0.9^n}{1-0.9}}$ (für $n = 1; 2; 3; ...$)
Bestätige diese Vorschrift, indem du 3 Werte berechnest und sie mit den Werten aus (a) vergleichst.
(d) Wie hoch wird der Turm, wenn man den Prozess „Würfel hinzufügen“ unendlich fortsetzt. Bestimme hierzu den Grenzwert der Folge $\left( a_n \right)$ durch Einsetzen großer $n$-Werte und mit geeigneten Überlegungen.
Aufgabe 4
Das Mengendiagramm soll verschiedene Mengen von Folgen verdeutlichen. Die Menge A steht hier für alle Folgen, die monoton sind, aber nicht beschränkt und nicht konvergent.
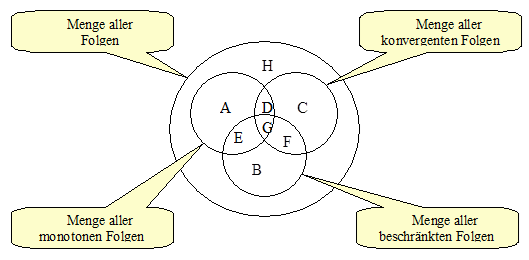
Ergänze Einträge in der Tabelle. Beachte: Es gibt hier Mengen, die leer sind (d.h. es gibt dann keine Beispielfolgen).
| Menge | Eigenschaften | Beispiel (Graph) |
|---|---|---|
| A | monoton nicht beschränkt nicht konvergent |
|
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
| G | ||
| H |

