Grenzwert der Folge

Das Grenzverhalten der Koffein-Folge untersuchen

Wir betrachten weiterhin die Koffein-Folge mit dieser Festlegung:

$a_n$: Menge an Koffein [in mg] im Körper unmittelbar nach der $n$-te Tasse Kaffee (für $n = 1; 2; 3; ...$)

Der Graph der Folge zeigt eine interessante Entwicklung.

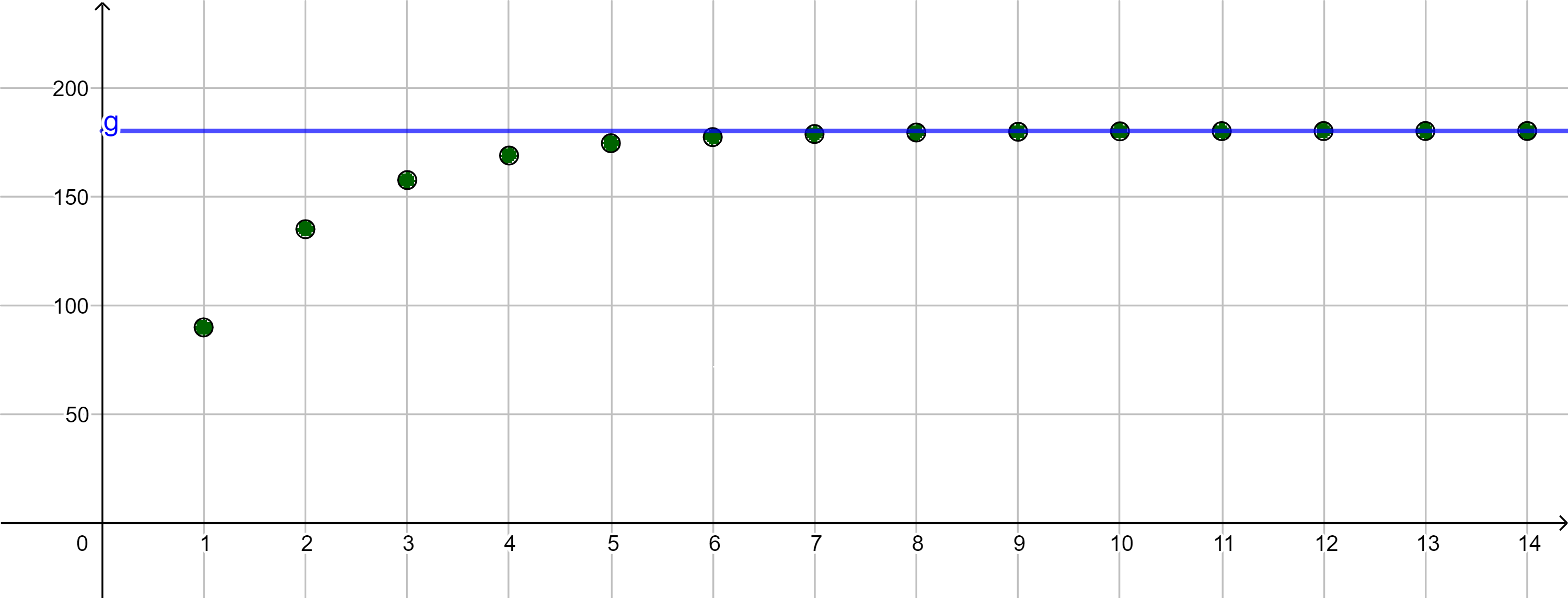
Die Folgenglieder stabilisieren sich mit wachsender Platznummer bei einem Grenzwert $g = 180$.

Das Grenzverhalten begründen - Version 1

Die Folgenglieder $a_1; a_2; ...$ der Koffeinfolge lassen sich mit einer rekursiven Darstellung berechnen:

$a_1 = 90$
$a_n = 0.5 \cdot a_{n-1} + 90$ für $n = 2; 3; ...$

Für die Folgenglieder gilt demnach:

$a_1 = 90$
$a_2 = 0.5 \cdot 90 + 90 = (1 + 0.5) \cdot 90$
$a_3 = 0.5 \cdot a_2 + 90 = 0.5 \cdot ((1 + 0.5) \cdot 90) + 90 = (1 + 0.5 + 0.5^2) \cdot 90$
$a_4 = ...$

Aufgabe 1

(a) Begründe die Umformungsschritte. Ergänze analoge Umformungen für $a_4$.

(b) Ergänze auch eine allgemeine Formel.

$a_n = ...$

Aufgabe 2

(a) Betrachte die Folge $\left( b_n \right)$ mit $b_n = 1 + 0.5 + 0.5^2 + ... + 0.5^{n-1}$ (für $n = 1; 2; 3; ...$).

Begründe mit Hilfe der Abbildung, dass $b_n$ mit wachsendem $n$ sich immer mehr dem Wert $2$ annähert.

(b) Nutze das Ergebnis aus (a), um das Grenzverhalten der Koffeinfolge zu begründen.

Das Grenzverhalten begründen - Version 2

Die Folgenglieder $a_1; a_2; ...$ der Koffeinfolge lassen sich auch mit einer expliziten Darstellung berechnen:

$a_n = 180 \cdot (1 - 0.5^n)$ für $n = 1; 2; 3; ...$

(a) Überprüfe exemplarisch, ob die explizite Darstellung tatsächlich die korrekten Werte liefert. Berechne hierzu mindestens 3 Folgenglieder mit der expliziten Darstellung.

(b) Nutze die explizite Darstellung, um das Grenzverhalten der Koffeinfolge zu begründen.