Erkundung - Drohnenshow

Ein Netz aus Drohnen

Eine Drohnenshow soll mit Hilfe vieler Drohnen eine Art Gitternetz am Himmel erzeugen. Die Drohnen sollen dabei wie im Applet zu sehen gleichmäßig angeordnet sein.

Zum Herunterladen: drohnen1.ggb

Ziel ist es, die Positionen der Drohnen genau festzulegen.

Aufgabe 1

Die Koordinaten der folgenden Drohnen werden vorgegeben.

• $D_{(0,0)}(0|1|4)$
• $D_{(1,0)}(-0.5|2|4)$
• $D_{(0,1)}(-0.5|1|4.5)$

(a) Bestimme die Koordinaten der Drohnenpunkte $D_{(2,0)}$, $D_{(3,0)}$ und $D_{(-1,0)}$.

(b) Bestimme die Koordinaten der Drohnenpunkte $D_{(0,2)}$, $D_{(0,3)}$ und $D_{(0,-1)}$.

(c) Bestimme die Koordinaten der Drohnenpunkte $D_{(1,1)}$, $D_{(3,2)}$, $D_{(-2,-1)}$. Erkläre, wie du dabei vorgehst.

(d) Mit dem folgenden Applet kannst du die Ergebnisse aus den vorherigen Teilaufgaben selbst kontrollieren. Gib hierzu die Koordinaten der Punkte im Algebrafenster unten ein.

Zum Herunterladen: drohnen2.ggb

Aufgabe 2

(a) Betrachte die folgenden vorgegebenen Vektoren.

• $\overrightarrow{q}=\overrightarrow{O{D}_{(0,0)}}=\left(\begin{array}{c}0\\ 1\\ 4\end{array}\right)$,
• $\overrightarrow{v}=\overrightarrow{D_{(0,0)}{D}_{(1,0)}}=\left(\begin{array}{c}-0.5\\ 1\\ 0\end{array}\right)$ und
• $\overrightarrow{w}=\overrightarrow{D_{(0,0)}{D}_{(0,1)}}=\left(\begin{array}{c}-0.5\\ 0\\ 0.5\end{array}\right)$.

Welche Drohnenpunkte lassen sich mit den folgenden Vektorkombinationen bestimmen?

• $\overrightarrow{q}+2\cdot \overrightarrow{v}+2\cdot \overrightarrow{w}$
• $\overrightarrow{q}+3\cdot \overrightarrow{v}+1\cdot \overrightarrow{w}$
• $\overrightarrow{q}+0\cdot \overrightarrow{v}-\overrightarrow{w}$
• $\overrightarrow{q}+(-2)\cdot \overrightarrow{v}+(-1)\cdot \overrightarrow{w}$

(b) Entwickle eine Formel zur Berechnung des Vektors $\overrightarrow{O{D}_{(r,s)}}$ aus den Vektoren $\overrightarrow{q}$, $\overrightarrow{v}$ und $\overrightarrow{w}$.

$\overrightarrow{O{D}_{(r,s)}}=...$ (wobei $r$ und $s$ für beliebige ganze Zahlen stehen)

Aufgabe 3

Auf der Seite beetleblocks.com findest du eine Programmierumgebung, mit der man u.a. die Bewegung eines Käfers im 3D-Raum steuern kann.

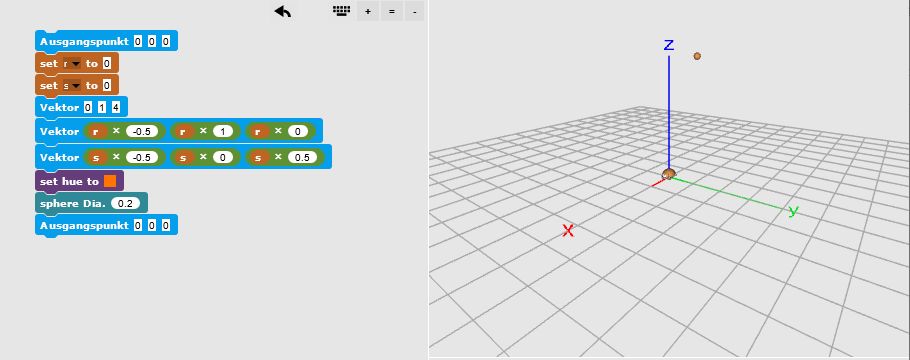
(a) Importiere die Datei drohnen2.xml. Mit den Blöcken [Vektor] und [Ausgangspunkt] kannst du die Bewegung eines (fliegenden) Käfers festlegen. Vorgegeben ist hier ein Programm, mit dem der Käfer eine Drohne im Raum positionieren kann. Analysiere das Programm und erkläre, wie es funktioniert. Benutze das Programm, um ein (ggf. eigenes) Gitternetz aus Drohnen zu erzeugen.

(b) Finde heraus, wo du die einzelnen Bestandteile der Berechnungsvorschrift aus Aufgabe 2 (b) in der Bewegung des Käfers wiederfindest. Beschreibe dann für jeden einzelnen Bestandteil der Vorschrift (Vektoren $\overrightarrow{q}$, $\overrightarrow{v}$ und $\overrightarrow{w}$ sowie Parameter $r$ und $s$), wo er im Programm zu finden ist und welche Funktion er zur Beschreibung der Gitterpunkte einnimmt.