Zusammenhang zum zweiten Strahlensatz
Wiederholung: Zweiter Strahlensatz
Es gibt einen Zusammenhang von der betrachteten Figur zum zweiten Strahlensatz. Doch was sagt der nochmal?
Aufgabe 1: Wiederholung
Wiederhole, was der zweite Strahlensatz aussagt. Formuliere ihn für folgende Figur.
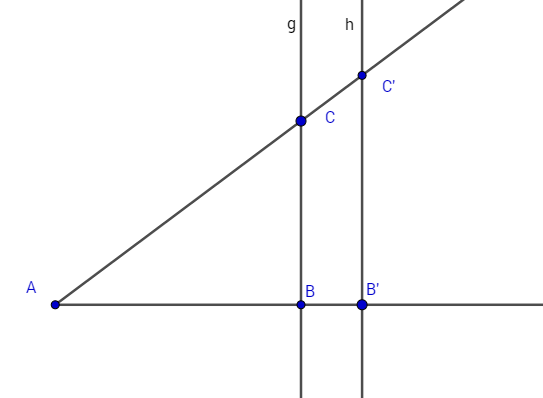
Anwendung auf die Situation am Einheitskreis
Wir kommen zurück zum bekannten Applet. Hier wirst du in der nächsten Aufgabe den zweiten Strahlensatz anwenden.
Zum Herunterladen: einheitskreis_3.ggb
Aufgabe 2: Anwendung
Falls du das vorherige Unterkapitel zu Zusammenhängen der Winkelfunktionen bearbeitet hast, wird dir das Ergebnis dieser Aufgabe bekannt vorkommen. Du solltest sie allerdings dennoch bearbeiten, weil hier aus einem anderen Blickwinkel heraus argumentiert wird. Zugleich bietet es sich an, die noch einmal klarzumachen, wie man ohne Einheitskreis zu denselben Ergebnissen gekommen ist.
Versuche selbst, den Strahlensatz anzuwenden, um zu einem Zusammenhang zwischen Sinus, Kosinus und Tangens zu kommen. Betrachte erst danach die Aufgabenteile.
(a) Der zweite Strahlensatz lässt sich so formulieren: Weil $g$ und $h$ parallel sind, gilt: $$\frac{|AB|}{|AB'|} = \frac{|AC|}{|AC'|} = \frac{|BC|}{|B'C'|}$$ Von diesen Streckenlängen sind einige bekannt und andere nicht. Setze alle bekannten Größen ein.
(b) In (a) sind drei Brüche aufgeführt, die alle den gleichen Wert haben. Einer der Brüche ist nicht interessant, weil in ihm keine Winkelfunktion vorkommt. Lasse ihn weg und formuliere die Gleichheit der anderen beiden Brüche.
(c) Stelle um, damit du eine Gleichung der Form $\tan(\alpha) = \dots$ erhältst. Das ist ein wichtiger Zusammenhang zwischen den drei Winkelfunktionen.
(d) Man braucht unsere Einheitskreisfigur gar nicht, um diesen Zusammenhang zu beweisen. Ersetze jede Winkelfunktion durch ihre Definition (also z.B. $\sin(\alpha)$ durch $\frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse}}$) und zeige damit den Zusammenhang, den du bereits in Teil (c) gefunden hast.

