Winkelfunktionen – Eine geometrische Sicht
Worum geht es hier?
Beispiel: Betrachte das Dreieck rechts.
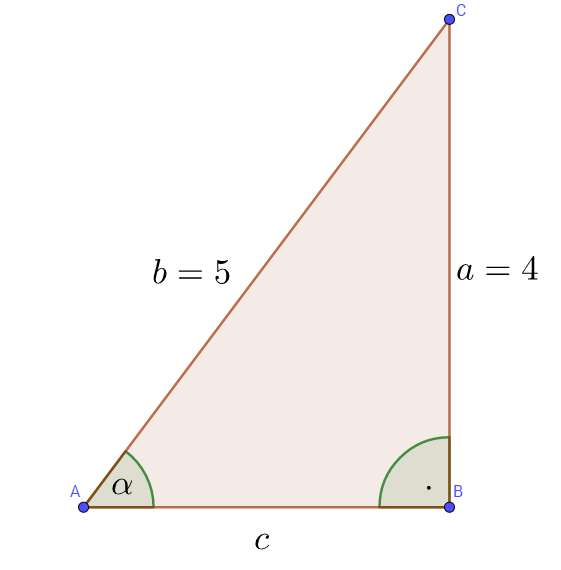
Einige Werte sind gegeben, andere nicht. Du hast bereits Wege kennengelernt, wie du weitere Werte bestimmen kannst:
- Mit dem Satz über die Winkelsumme kannst du den dritten Winkel bestimmen, sofern du $\alpha$ kennst.
- Mit dem Satz des Pythagoras kannst du die dritte Seite des Dreiecks ausrechnen. Mach dir klar, welche wichtige Eigenschaft des Dreiecks du hier benötigst.
- Mit einer maßstabsgetreuen Zeichnung kannst du die Winkel ausmessen. Du nutzt dabei die Ähnlichkeit von Dreiecken aus.
Wenn wir Winkel kennen, können wir andere Winkel berechnen. Wenn wir Seitenlängen kennen, können wir andere Seitenlängen berechnen. Aber was, wenn wir Winkel kennen und uns für Seitenlängen interessieren? Oder wenn wir Seitenlängen kennen (wie im Beispiel oben) und Winkel (hier z.B. $\alpha$) wissen wollen? Dann hilft uns bisher nur Zeichnen und Messen – mit allen Nachteilen, die eine solche geometrische Lösung mit sich bringt.
In diesem Kapitel erforschen wir deshalb den Zusammenhang zwischen den Seitenlängen und den Winkeln eines Dreiecks, um Wege zu finden, auch solche Probleme rechnerisch zu lösen.
Für dieses Thema musst du wissen, ...
- ... was man unter der Ähnlichkeit von Dreiecken versteht.
- ... wie man mit dem Satz von Pythagoras unbekannte Seitenlängen eines rechtwinkligen Dreiecks berechnet.
Hier lernst du, ...
- ... wie man die einzelnen Seiten in einem rechtwinkligen Dreieck bezeichnet.
- ... wie die drei Winkelfunktionen definiert sind.
- ... wie du mithilfe der Winkelfunktionen unbekannte Seitenlängen in einem rechtwinkligen Dreieck bestimmen kannst.

