Strukturierung – Neue Namen für die Dreiecksseiten
Zielsetzung
In der Erkundung hast du dich relativ lange mit rechtwinkligen Dreiecken auseinandergesetzt. Weil man das in der Mathematik häufig tun muss, hat man sich auf Namen für die einzelnen Dreiecksseiten geeinigt, um leichter darüber sprechen zu können.
Aufgabe 1: Was wir schon wissen
Bei der Behandlung des Satzes von Pythagoras hast du bereits allgemeine Namen für die Seiten im rechtwinkligen Dreieck kennengelernt.
(a) Vervollständige: „Bei einem rechtwinkligen Dreieck ist das Quadrat der $\dots$ so lang wie $\dots$.“
Du brauchst die Begriffe „Kathete“, „Summe“, „Hypotenuse“, „Quadrate“.
(b) Begründe, dass man den Satz des Pythagoras so formulieren sollte wie in Teil (a) statt nur die Formel $a²+b²=c²$ auswendig zu lernen.
Die Katheten unterscheiden
Für die Hypotenuse brauchen wir keinen neuen Namen, die ist ja bereits eindeutig festgelegt. Tatsächlich bedeutet Hypotenuse auch einfach „gegenüber dem rechten Winkel“. Aber die beiden Katheten können wir mit unseren Begriffen noch nicht unterscheiden, obwohl sie je nach Situation ganz unterschiedliche Funktionen haben.
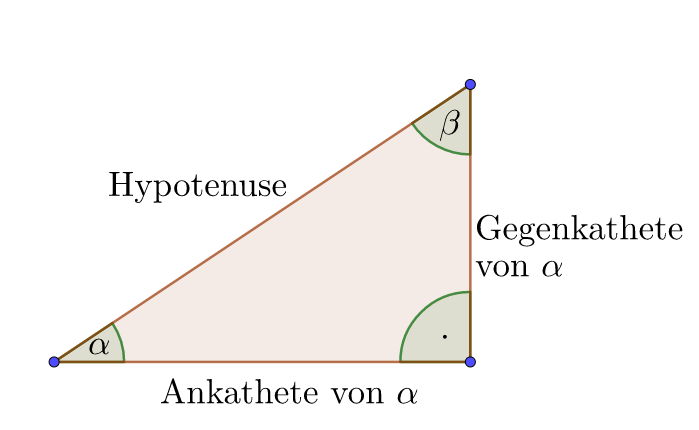In einem rechtwinkligen Dreieck, bei dem $\alpha$ einer der beiden spitzen Winkel ist, bezeichnen wir die Kathete, die an $\alpha$ anliegt als Ankathete von $\alpha$. Die Kathete, die dem Winkel gegenüberliegt, bezeichnen wir als Gegenkathete von $\alpha$. Die Seite gegenüber des rechten Winkels bezeichnen wir weiterhin als Hypotenuse des Dreiecks.
Aufgabe 2: Neue Begriffe anwenden
Im vorherigen Abschnitt wurde eine Straße betrachtet.
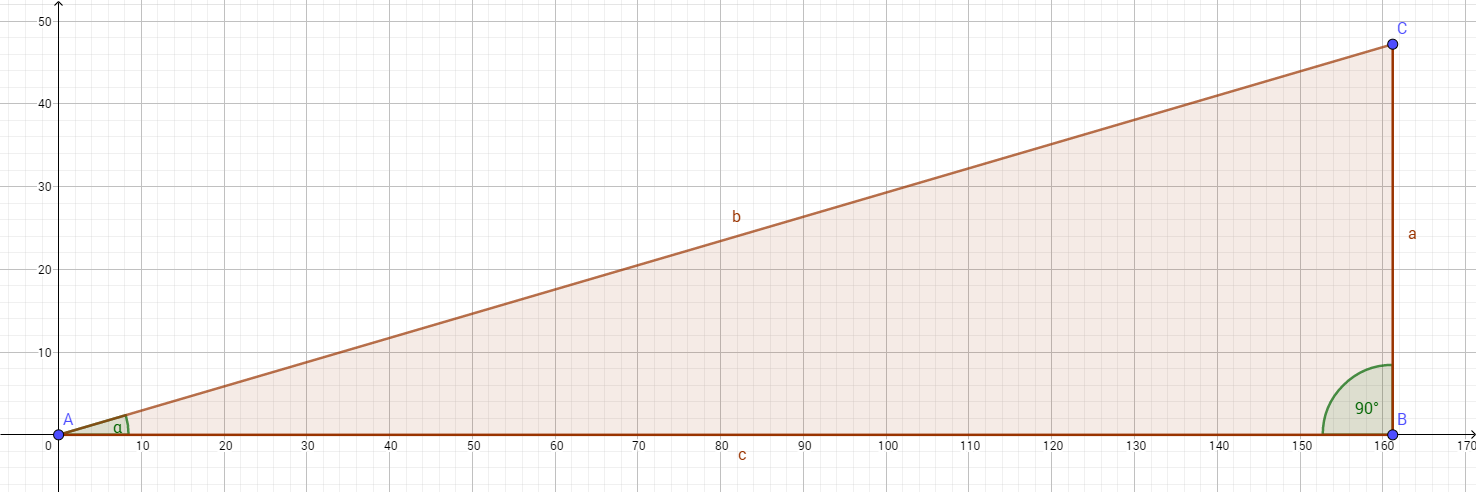
(a) Nenne für jede der drei Dreiecksseiten den Fachbegriff.
(b) Vervollständige diese Formulierung: „Die Steigung des Dreiecks berechnen wir, indem wir die $\dots$ durch die $\dots$ dividieren.“
(c) Ist dir aufgefallen, dass es „An-/Gegenkathete von $\alpha$“ heißt, aber „Hypotenuse des Dreiecks“? Erkläre, warum man z.B. bei der Ankathete nicht einfach „des Dreiecks“ sagen kann.
Wie sieht das für den anderen Winkel aus?
Wir haben bisher immer alles vom Winkel $\alpha$ aus betrachtet. Doch wie sieht es für $\beta$ aus?
Aufgabe 3: Aus der Sicht von $\beta$
Ordne im Applet die Beschriftungen den drei Dreiecksseiten zu.
Zum Herunterladen: dreiecksseiten2.ggb
Das Wichtigste notieren
Du solltest dir nun das Wichtigste, was du gerade gelernt hast, notieren.
Aufgabe 4: Eine Zusammenfassung
Fasse das Wichtigste selbst schriftlich zusammen. Die folgenden Anregungen können dir dabei helfen:
- Nutze als Überschrift „Bezeichnungen für die Seiten im rechtwinkligen Dreieck“.
- Zeichne dir darunter ein eigenes beschriftetes Beispiel. Wenn die Bezeichnungen für beide spitzen Winkel des Dreiecks deutlich werden sollen, bietet es sich an, verschiedene Farben zu verwenden.
- Fasse auch in Worten kurz zusammen, was man unter der Ankathete und der Gegenkathete von $\alpha$ versteht. Besonders übersichtlich wird es, wenn du im Text dieselben Farben nutzt wie in der Skizze.
- Erkläre auch kurz, warum der Zusatz „von $\alpha$“ bzw. „von $\beta$“ bei den Katheten wichtig ist und bei der Hypotenuse nicht.
