Zusammenfassung – Winkelfunktionen
Bezeichnungen der Dreiecksseiten
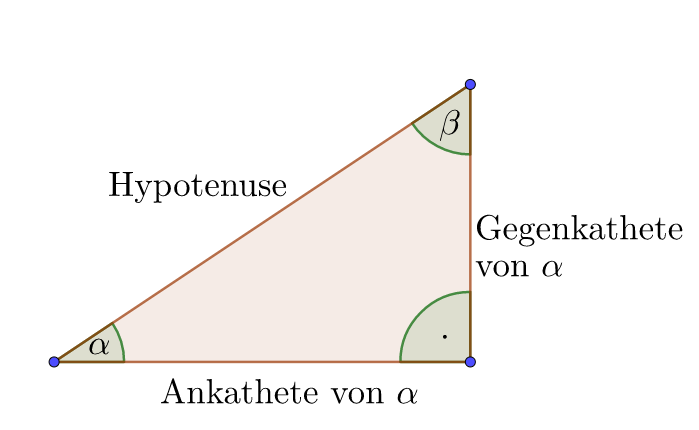In einem rechtwinkligen Dreieck, bei dem $\alpha$ einer der beiden spitzen Winkel ist, bezeichnen wir die Kathete, die an $\alpha$ anliegt als Ankathete von $\alpha$. Die Kathete, die dem Winkel gegenüberliegt, bezeichnen wir als Gegenkathete von $\alpha$. Die Seite gegenüber des rechten Winkels bezeichnen wir weiterhin als Hypotenuse des Dreiecks.
Beachte, dass die Hypotenuse nicht vom Winkel $\alpha$ abhängt. Man spricht also nicht von der „Hypotenuse von $\alpha$“. Anders sieht es bei den Katheten aus: Würde man nur „Ankathete des Dreiecks“ sagen, wäre nicht klar, an welchem der beiden spitzen Winkeln sie anliegt.
Die beiden spitzen Winkel eines rechtwinkligen Dreiecks stehen in einer gewissen Dualität zueinander: Die Ankathete des einen ist die Gegenkathete des anderen und umgekehrt:
Zum Herunterladen: dreiecksseiten3.ggb
Seitenverhältnisse im Dreieck
Sind zwei Dreiecke ähnlich (im Applet die oberen beiden), so sind sich entsprechende Seitenverhältnisse gleich. Ähnlichkeit liegt vor, wenn drei sich entsprechende Winkel übereinstimmen. Stimmen zwei sich entsprechende Winkel überein, so ist der dritte aufgrund des Winkelsummensatzes ebenfalls gleich. Auch dann sind die Dreiecke also ähnlich und Seitenverhältnisse gleich. Stimmt jedoch nur ein Winkel überein (im Applet beim unteren Dreieck), so kann daraus keine Ähnlichkeit geschlussfolgert werden. Also müssen Seitenverhältnisse dann auch nicht übereinstimmen.
Zum Herunterladen: seitenverhaeltnisse.ggb
In den Textfeldern im Applet werden gerundete Werte angezeigt, sodass manche Ergebnisse ggf. auf den ersten Blick falsch wirken.
Seitenverhältnisse im rechtwinkligen Dreieck
Nun betrachten wir nur noch rechtwinklige Dreiecke. Stimmen zwei rechtwinklige Dreiecke in einem weiteren Winkel überein, dann gilt das auch für den dritten Winkel (Winkelsummensatz), sodass sie ähnlich sind und Seitenverhältnisse übereinstimmen. Im Applet erkennst du das daran, dass sich die Verhältnisse nicht ändern, wenn du das Dreieck mit dem unteren Schieberegler vergrößerst/verkleinerst.
Zum Herunterladen: seitenverhaeltnisse-rechtwinklig.ggb
In den Textfeldern im Applet werden gerundete Werte angezeigt, sodass manche Ergebnisse ggf. auf den ersten Blick falsch wirken.
Winkelfunktionen
Für jedes der drei Seitenverhältnisse aus dem Applet oben kann man nun folgende Überlegung anstellen: Alle rechtwinkligen Dreiecke mit einem bestimmten Winkel $\alpha$ sind ähnlich zueinander. Also ist das Seitenverhältnis in all diesen Dreiecken gleich. Also können wir dem Winkel eindeutig das Seitenverhältnis zuordnen.
Aufgrund dieser Eindeutigkeit ist die Zuordnung von Winkel zu Seitenverhältnis also eine Funktion. Da der Ausgangswert der Funktion ein Winkel ist, nennt man die entsprechenden Funktionen Winkelfunktionen. Ein anderer Name dafür lautet trigonometrische Funktionen. Der Begriff Trigonometrie setzt sich aus den griechischen Wörtern für „Dreieck“ und „Maß“ zusammen und bezeichnet die Untersuchung von Zusammenhängen zwischen Seiten und Winkeln in Dreiecken.
In einem rechtwinkligen Dreieck und einem Winkel $\alpha\ne 90°$ definieren wir die folgenden drei Winkelfunktionen:
- Der Sinus von $\alpha$ ist der Quotient $$\sin(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse des Dreiecks}}.$$
- Der Kosinus von $\alpha$ ist der Quotient $$\cos(\alpha)=\frac{\text{Ankathete von }\alpha}{\text{Hypotenuse des Dreiecks}}.$$
- Der Tangens von $\alpha$ ist der Quotient $$\tan(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Ankathete von }\alpha}.$$
Werte für Winkelfunktionen
Früher hat man die Funktionswerte der Winkelfunktionen in großen Tabellen notiert, um sie daraus ablesen zu können. Das Prinzip wird/wurde auch bei anderen mathematischen Problemen verwendet, z.B. für Logarithmen und Wahrscheinlichkeitsverteilungen. Zur Bestimmung von Funktionswerten von Winkelfunktionen kann man entweder auf geometrische Überlegungen (exaktes Zeichnen und Ablesen) oder auf komplizierte mathematische Berechnungen zurückgreifen. Liegt der gesuchte Winkel zwischen zwei Winkeln in der Tabelle, so kann man den Funktionswert annähern: z.B. könnte man für den Sinus von $\alpha=30,5°$ den Mittelwert von $\sin(30°)$ und $\sin(31°)$ heranziehen.
Heute kann man die Funktionswerte mit dem Computer berechnen. Während es bei leistungsschwachen Computern und Echtzeit-Anwendungen hilfreich war, die Werte trotzdem aus einer vorab gespeicherten Tabelle abzulesen (geht schneller), bietet das heute kaum noch einen Vorteil.
Im Taschenrechner sind die Funktionswerte der Winkelfunktionen ebenfalls eingespeichert.
Es ist möglich, dass du mit dem Taschenrechner komplett falsche Ergebnisse heraus bekommst. Dann ist er vermutlich auf das Bogenmaß (oft „RAD“) und nicht auf das Gradmaß (oft „DEG“) eingestellt. Das ist eine andere Art, wie man die Größe von Winkeln beschreiben kann. Wir gehen darauf später noch genauer ein. Fürs erste solltest du nur herausfinden, wie du deinen Taschenrechner ins Gradmaß einstellst.
Problemlösung mit Winkelfunktionen
Die Winkelfunktionen können eingesetzt werden, um unbekannte Größen eines Dreiecks zu bestimmen – vorausgesetzt, man kennt den Wert der Winkelfunktion für den betrachteten Winkel.
Oft funktioniert folgendes Vorgehen:
- Notiere mit Fachbegriffen, welche Größen des Dreiecks gegeben und welche gesucht sind.
- Suche die passende Winkelfunktion heraus, die diue gegebenen und gesuchten Werte enthält.
- Stelle die Definition der Winkelfunktion nach der gesuchten Größe um.
- Setze die bekannten Größen ein. Dafür musst du den Wert der Winkelfunktion z.B. mit dem Applet von Aufgabe 2 bestimmen.
- Interpretiere das Ergebnis im Sachzusammenhang.
Beispiel: Wir wollen eine Mauer überwinden und haben die passende Leiter dabei, um sie in einem Anstellwinkel von $70°$ anzustellen. Die Leiter ist $6$ m lang. Doch wie weit von der Mauer entfernt müssen wir sie am Boden aufstellen?
geg: rechtwinkliges Dreieck mit Winkel $\alpha$, Hypotenuse des Dreiecks (Leiterlänge) $b=6$ m.
ges: Ankathete $c$ von $\alpha$
Lsg:
Die passende Winkelfunktion ist $$\cos(\alpha) = \frac{\text{Ankathete von }\alpha}{\text{Hypotenuse des Dreiecks}}=\frac{c}{b}.$$
Eine Multiplikation mit dem Nenner und der Tausch der beiden Seiten ergibt $$c = b \cdot \cos(\alpha).$$
Mit dem Applet erhalten wir $\cos(70°) \approx 0,34$; die Hypotenuse ist $6$ m lang. Einsetzen ergibt: $$c \approx 6 \text{ m} \cdot 0,34= 2,04 \text{ m}.$$
Antwort: Man sollte die Leiter ca. $2,04$ m von der Mauer entfernt aufstellen.
Umkehrung der Winkelfunktionen
Durch Ausprobieren wird es plausibel, dass man die Winkelfunktionen umkehren kann. Ohne Beweis halten wir diese Aussage deshalb fest:
Wann ein Seitenverhältnis „zulässig“ ist, müssen wir noch klären.
Da die Winkelfunktionen umkehrbar sind, können wir ihren Umkehrungen auch Namen geben: Sie werden Arkussinus, Arkuskosinus und Arkustangens genannt. Man schreibt dafür $\arcsin(\alpha)$, $\arccos(\alpha)$ bzw. $\arctan(\alpha)$.
Quellen
-
[1]: Leiter - Urheber: FR - Lizenz: inf-schule.de
unter Verwendung von:
- Holzleiter - Urheber: Susannehs - Lizenz: Pixabay Licence
