Erkundung – Leitern

Belagerungen

Im Bild wird die Belagerung von Konstantinopel dargestellt. Vor der Verbreitung von Kanonen und Artellerie waren Stadtmauern ein schwer zu überwindendes Hindernis. Deshalb haben die Kriegsingenieure des Mittelalters verschiedene Belagerungsmaschinen entwickelt: Katapulte, um über die Mauer zu schießen; Rammböcke, um Tore aufzubrechen; Belagerungstürme, um die Mauer zu erklimmen; ... Eine sehr einfache Methode sind jedoch Leitern, um auf die Stadtmauer zu gelangen – schließlich nutzen wir diese noch heute, um an hoch gelegene Orte zu kommen. Auch dabei wurden allerlei Optimierungen angestellt, z.B. sogenannte Sturmleitern, die man im Gefecht zusammenstecken konnte und die oben mit Haken versehen war, um mehr Halt zu finden. Wir beschränken uns hier jedoch auf ganz einfache Leitern, wie sie im Bild zu sehen sind.

Ein stabiler Stand

Wenn man eine Leiter an eine Wand stellt, ist der Anstellwinkel $\alpha$ entscheidend. Ist er zu klein gewählt, ist das Risiko sehr groß, dass die Leiter beim Besteigen wegrutscht. Ist er zu groß gewählt, kann die Leiter durch eine Krafteinwirkung am oberen Ende einfach umgeworfen werden; das ist gerade bei der Erstürmung einer Stadt nicht empfehlenswert. Empfohlen wird oft ein Winkel $\alpha$ von $70°$.

Wenn wir nun mit Leitern Städte einnehmen wollen, müssen wir das sorgfältig planen: Unsere Spione müssen zuerst herausfinden, wie hoch die Stadtmauern sind. Dann müssen wir berechnen, wie lange Leitern wir bauen sollten. Erst dann können wir in die Schlacht ziehen. Mit zu kurzen Leitern können wir die Mauern nicht erklimmen oder wir werden von den Verteidigern einfach zurückgeschubst. Mit zu langen Leitern ist die Gefahr zu groß, dass sie unter dem Gewicht eines Ritters in Rüstung durchbricht.

Aufgaben

Aufgabe 1: Belagerung von Konstantinopel

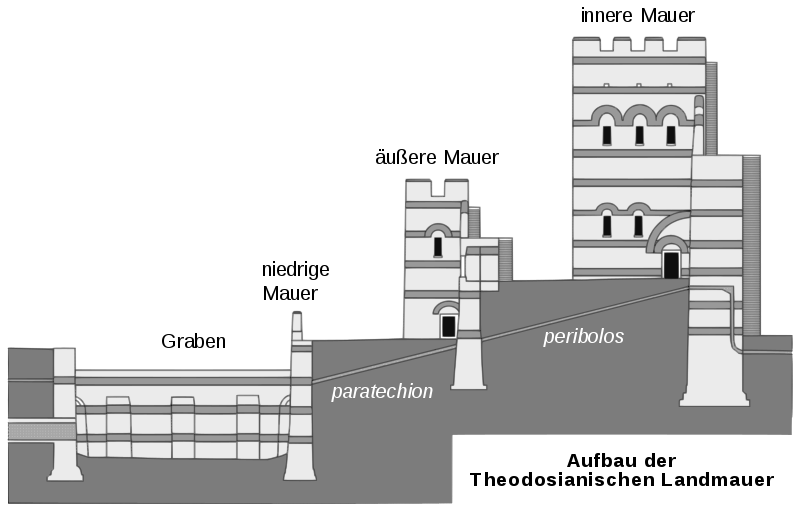
Um Konstantinopel wurde im fünften Jahrhundert auf Befehl von Kaiser Theodosius eine sehr durchdachte Befestigungsanlage errichtet, um die Stadt vor den Hunnen zu schützen. Die Anlage besteht aus mehreren Mauern, Türmen und Gräben.

(a) Wir betrachten zuerst die mittlere der drei Mauern. Sie war etwa 8 Meter hoch. Zeichne eine maßstabgetreue Skizze des Dreicks, das von Mauer und Leiter gebildet wird. Nutze als Höhe der Mauer 8 cm. Achte auf den Winkel von $70°$. Beschrifte das Dreieck mit den Fachbegriffen „Hypotenuse“, „Ankathete von $\alpha$“ und „Gegenkathete von $\alpha$“. Lese dann die nötige Länge der Leiter ab.

(b) Die anderen beiden Mauern waren 2 bzw. 12 Meter hoch. Bestimme auch hier die benötigte Leiterlänge durch maßstabgetreue Zeichnungen.

(c) Chris hat das Dreieck für die kleinste der Mauern gezeichnet und dabei als Höhe 2 cm genutzt. Beim Ablesen kommt er auf eine Hypotenuse von 2 cm, also einer Leiterlänge von 2 Metern. Er erkennt direkt, dass das nicht stimmen kann. Erkläre mit den Eigenschaften eines Dreiecks, warum das falsch sein muss. Erkläre, wie es zu dem Fehler gekommen ist und warum er ausgerechnet bei dieser Mauer auftritt und nicht bei einer der anderen beiden.

(d) Dani sagt, dass sie einen besonders cleveren Weg gefunden hat, das Problem zu lösen: Sie hat die mittlere Mauer wie in Teil (a) im Maßstab von $1:100$ gezeichnet, also aus einem Meter einen Zentimeter gemacht. Für die kleine Mauer hat sie einen Maßstab von $1:25$ gewählt; aus einem Meter werden damit 4 cm. Welchen Maßstab hat sie vermutlich für die dritte Mauer gewählt? Warum ist das clever?

(e) Zum Erinnern: Warum konnte man mit den Informationen aus Teil (a) (Anstellwinkel, Mauerlänge, rechter Winkel) das Dreieck zeichnen? Welcher Satz wurde verwendet?

Aufgabe 2: Den Feldzug fortsetzen

Nachdem wir Konstantinopel erfolgreich eingenommen haben, wollen wir noch weitere historische Mauern überwinden. Die chinesische Mauer ist teilweise 6, teilweise 9 Meter hoch. Die Mauern von Babylon waren sogar 30 Meter hoch. Die Höhe der Berliner Mauer betrug ungefähr 3,60 Meter – ganz ähnlich zum Limes der alten Römer. Und dann gibt es da noch Mauern aus der Fantasy-Welt: Die Eismauer aus Game of Thrones trennt mit ihren 200 Metern Höhe den Norden von den sieben Königslanden ab.

Zum Entdecken: Findest du selbst einen Weg, wie du für all diese Mauern die nötige Leiterlänge bestimmen kannst? Der Rest der Aufgabe führt dich schrittweise zu einer Lösung.

Zeige den Rest