Strukturierung – Sinus- und Kosinusfunktion
Winkelfunktionen im Gradmaß
In der Erkundung hast du festgestellt, dass man den Definitionsbereich von Sinus und Kosinus auch auf mehr als $90°$ erweitern kann. Tatsächlich kann man jedem beliebigen Winkel einen Sinus- und Kosinuswert zuweisen. Dafür nutzt man die Darstellung am Einheitskreis.
Die Winkelfunktionen $\sin(\alpha)$ und $\cos(\alpha)$ ordnen jedem Winkel $\alpha$ die Koordinaten eines umlaufenden Punktes auf einem Einheitskreis zu.
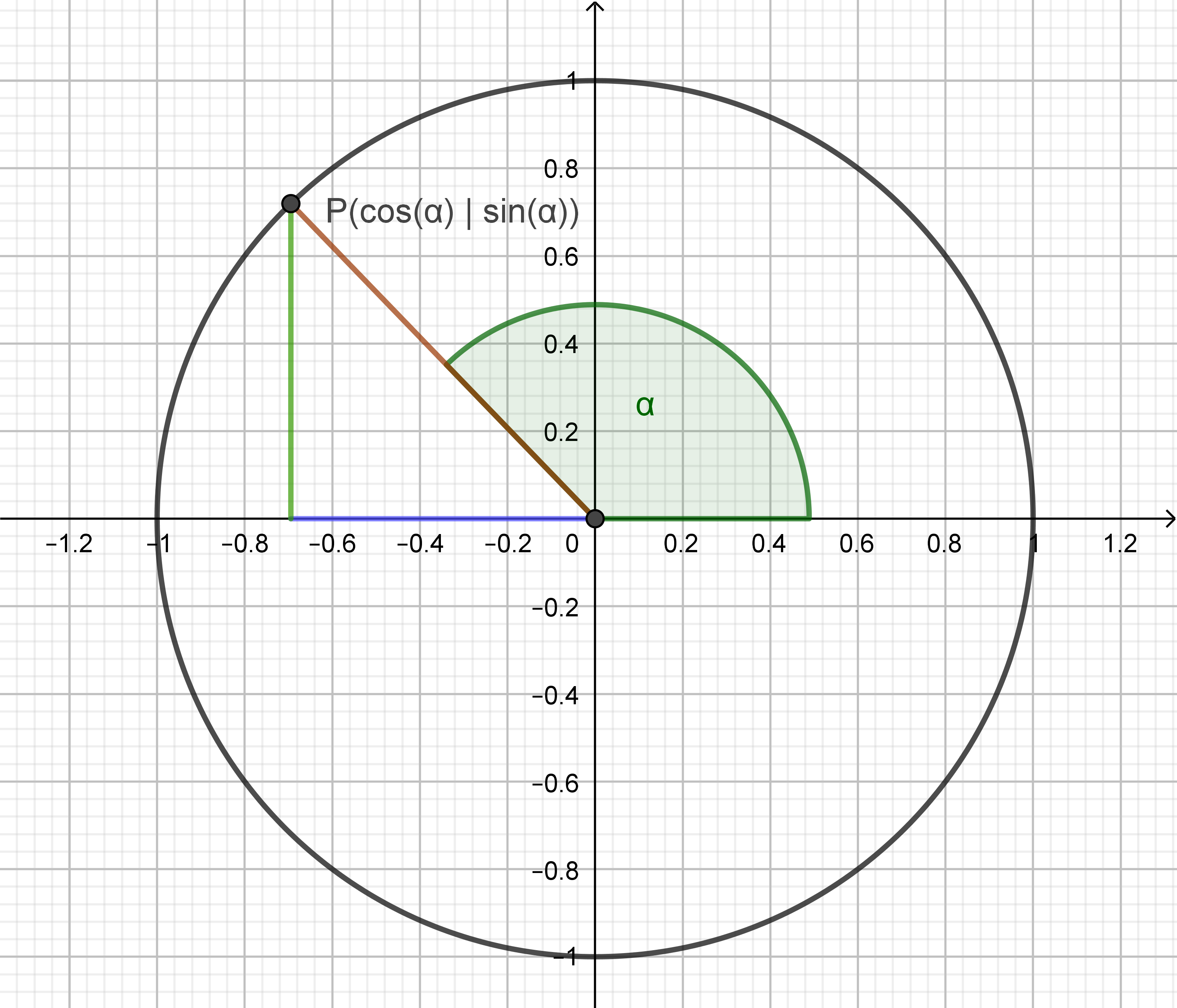
Beachte, dass diese Definition für die Winkel von $0°$ bis $90°$ dieselben Werte liefert wie die Definition mithilfe rechtwinkliger Dreiecke. Das wurde im Abschnitt Winkelfunktionen am Einheitskreis gezeigt. Die Funktionswerte der Sinus- und Kosinusfunktion liegen aufgrund der Definition im Intervall $[-1, 1]$.
Zum Herunterladen: trigonometrische-fkt-gradmass.ggb
Aufgabe 1
Erstelle mithilfe des Applets eine Wertetabelle für den Sinus und Kosinus. Suche dir hierfür „charakteristische Werte“ heraus (z.B.: Welcher Funktionswert liegt bei 45°, 90° usw. vor? Wann ist der Funktionswert 0, 0.5, 1?).
Eine Besonderheit dieser Funktionen ist, dass sich die Funktionswerte immer wieder wiederholen, sobald man $360°$ „weitergeht“. Es gilt also zum Beispiel $\sin(420°) = \sin(60°)$, weil $420° = 60° + 360°$. Man kann den Zusammenhang so in Formeln ausdrücken:
Für alle $k \in \mathbb{Z}$ gilt $\sin(\alpha) = \sin(\alpha + k\cdot 360°)$ sowie $\cos(\alpha) = \cos(\alpha + k\cdot 360°)$.
Man nennt die Sinus- und Kosinusfunktion daher periodisch mit der Periode $360°$.
Aufgabe 2
Recherchiere, wo die Begriffe „Periode“ und „periodisch“ innerhalb und außerhalb der Mathematik noch vorkommen. Haben sie dabei eine ähnliche Bedeutung?
Winkelfunktionen im Bogenmaß
Es ist sehr untypisch, dass die $x$-Werte einer Funktion Winkel sind. Normalerweise definieren wir Funktionen so, dass sie reelle Zahlen auf reelle Zahlen abbilden. Wenn wir aber die Winkel nicht im Gradmaß, sondern im Bogenmaß betrachten, dann erhalten wir Funktionen von $\mathbb{R}$ nach $\mathbb{R}$.
Die Winkelfunktionen $\sin(x)$ und $\cos(x)$ ordnen jeder reellen Zahl $x$ die Koordinaten eines umlaufenden Punktes auf einem Einheitskreis zu, wobei $x$ als Winkel im Bogenmaß aufgefasst wird.
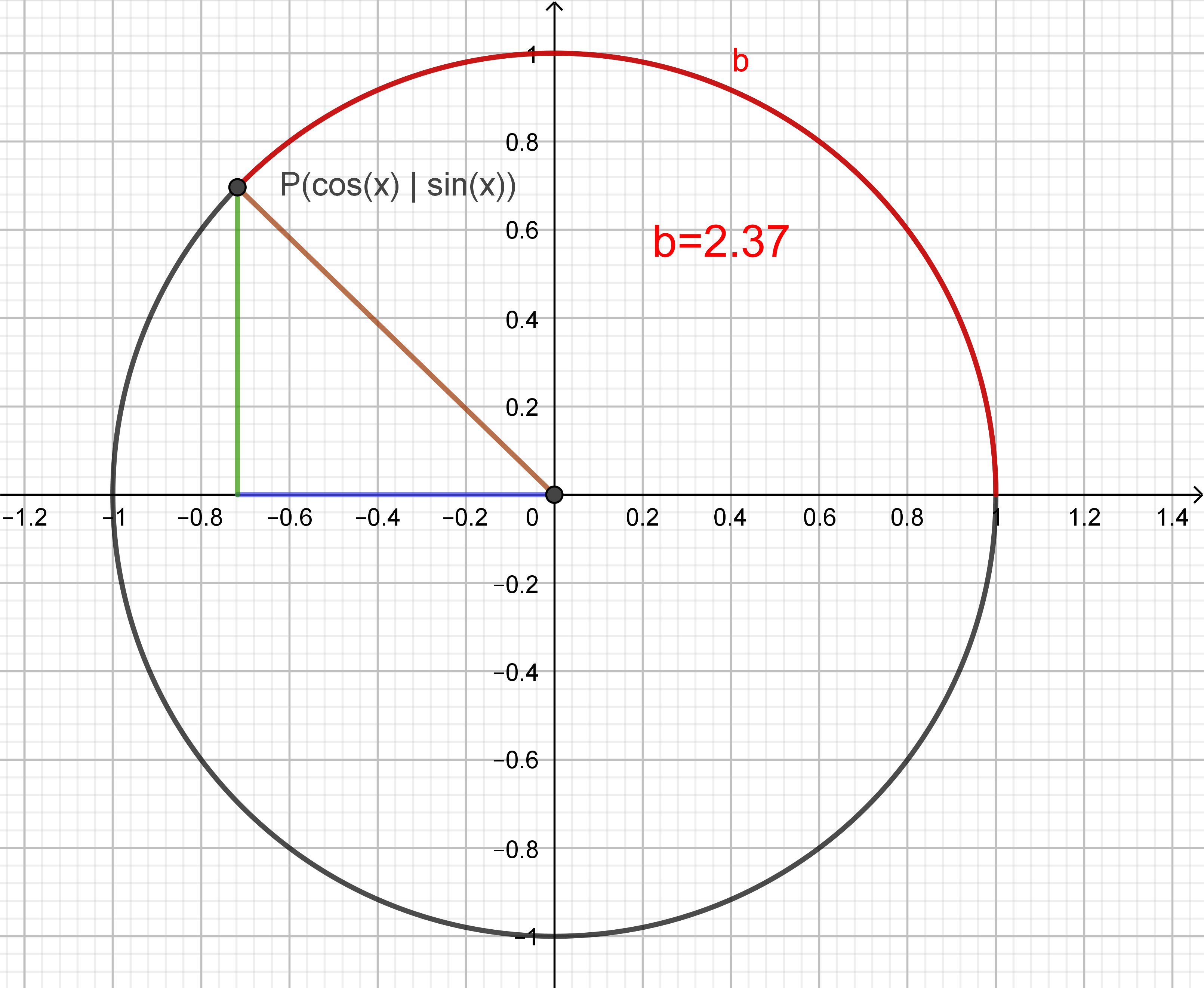
Im folgenden Applet kann der Punkt $P$ verschoben werden.
Zum Herunterladen: trigonometrische-fkt-bogenmass.ggb
Aufgabe 3
Betrachte deine Tabelle aus Aufgabe 1 und ergänze sie um die entsprechenden Werte im Bogenmaß. Damit hast du eine Wertetabelle für $\sin(x)$ und $\cos(x)$. Vergleiche mit dem Applet oben.
Aufgabe 4
Natürlich sind auch $\sin(x)$ und $\cos(x)$ periodische Funktionen. Was ist hier (im Bogenmaß) nun die Periode? Formuliere die Aussage als Satz, so wie oben beim Gradmaß.
Untersuchung der Graphen
Wie bei anderen Funktionen auch, lohnt es sich, die Gestalt der Graphen betrachten.
Aufgabe 5
Nutze das Applet oben, um die Graphen genauer zu analysieren:
- Analysiere die Symmetrie: Eine der Funktionen ist achsensymmetrisch zur $y$-Achse und eine ist punktsymmetrisch zum Ursprung. Auf welche trifft was zu?
- Analysiere die Vorzeichen und Nullstellen: Für welche Zahlen $x$ ist $\sin(x)$ bzw. $\cos(x)$ gleich null? Wann sind die Funktionswerte positiv, wann negativ?
- Zusammenhang von Sinus und Kosinus: Man kann den Graphen des Kosinus erhalten, indem man den Graphen des Sinus etwas verschiebt. Um wieviel muss er entlang der $x$-Achse verschoben werden?

