Erkundung – Steigung einer Straße

Was bedeutet dieses Schild?

Aufgabe 1

Was bedeutet dieses Schild?

(a) Versuche aus der Erinnerung heraus, zu formulieren, was das Straßenschild aussagt.

(b) Wir versuchen, das zu präzisieren: Formuliere die Aussage des Verkehrsschildes mithilfe dieses Dreiecks.

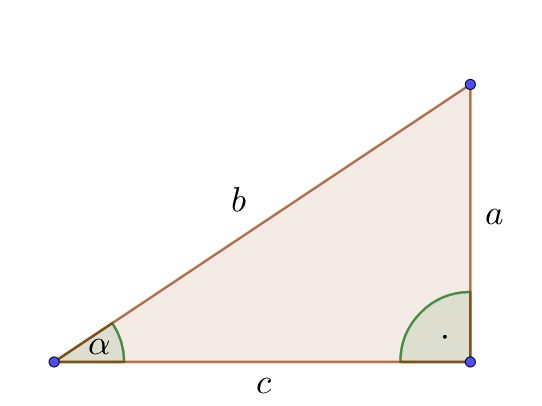
(c) Wir haben eine Klasse gefragt, was das Schild aussagt, und haben verschiedene Antworten erhalten. Manche Schüler:innen haben ihre Vermutung in Worten ausgedrückt, andere in der „Sprache der Mathematik“. Ordne jeweils einander zu.

(d) Was entspricht nun der Bedeutung des Straßenschildes? Wenn möglich, diskutiere mit anderen. Falls ihr euch nicht einigen könnt, recherchiert im Internet.

Die steilste Straße

Besonders steile Straßen haben viele Nachteile: Es ist schwieriger, sie zu Fuß, mit dem Rad oder auch mit einem voll beladenen Auto hinaufzufahren. Beim Parken muss man auf jeden Fall die Handbremse anziehen, damit das Auto nicht wegrollt. Und das Anfahren am Berg ist natürlich auch schwieriger, je steiler die Straße ist. So verwundert es nicht, dass viele steile Straßen durch Serpentinen abgeflacht worden sind, z.B. die Lombard Street in San Francisco, die du rechts sehen kannst.

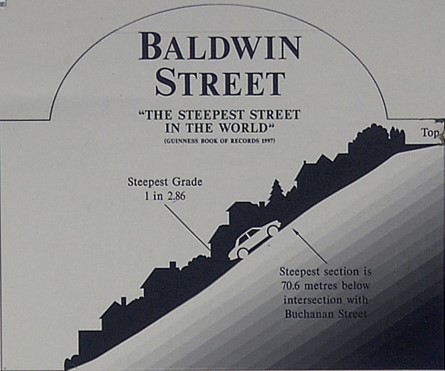
Eine besonders steile Straße kann jedoch auch eine Attraktion sein. Bei der steilsten Straße der Welt ist das auf jeden Fall so: Die Baldwin Street in Neuseeland wird vom Guinness-Buch der Rekorde als steilste Straße geführt und hat an ihrer steilsten Stelle eine Steigung von $1:2,86$. Das bedeutet: Pro 2,86 Meter, die man in horizontaler Richtung zurücklegt, bewegt man sich um einen Meter nach oben. Zu Beginn steigt die Straße noch recht moderat an. Im oberen Abschnitt der Straße hat sie über 150 Meter lang eine durchschnittliche Steigung von knapp 30%.

Aufgabe 2

Man kann Steigungen auf verschiedene Arten beschreiben: Als Winkel, als Verhältnis (auch Gradient oder auf englisch „Grade“, z.B. $1:2,86$) oder in Prozent (z.B. 30%).

(a) Der Gradient ist letztlich einfach ein Bruch: $\frac{1m}{2,86m}$. Beschreibe mithilfe des Textes oberhalb der Aufgabe, was der Zähler und der Nenner des Bruchs aussagen. Berechne dann den Wert des Bruchs als Dezimalzahl und stelle sie in Prozentschreibweise dar. Du kennst nun die maximale Steigung (in Prozent) der steilsten Straße der Welt.

(b) Für den oberen Abschnitt der Straße sind folgende Werte angegeben: Man bewegt sich 161,2 Meter horizontal und dabei 47,2 Meter nach oben. Schreibe dies auf gleiche Weise als Bruch. Kürze ihn so, dass du ein Verhältnis der Form $1:\dots$ erhältst. Berechne dann die Steigung in Prozent und vergleiche mit der Angabe im Text oberhalb der Aufgabe.

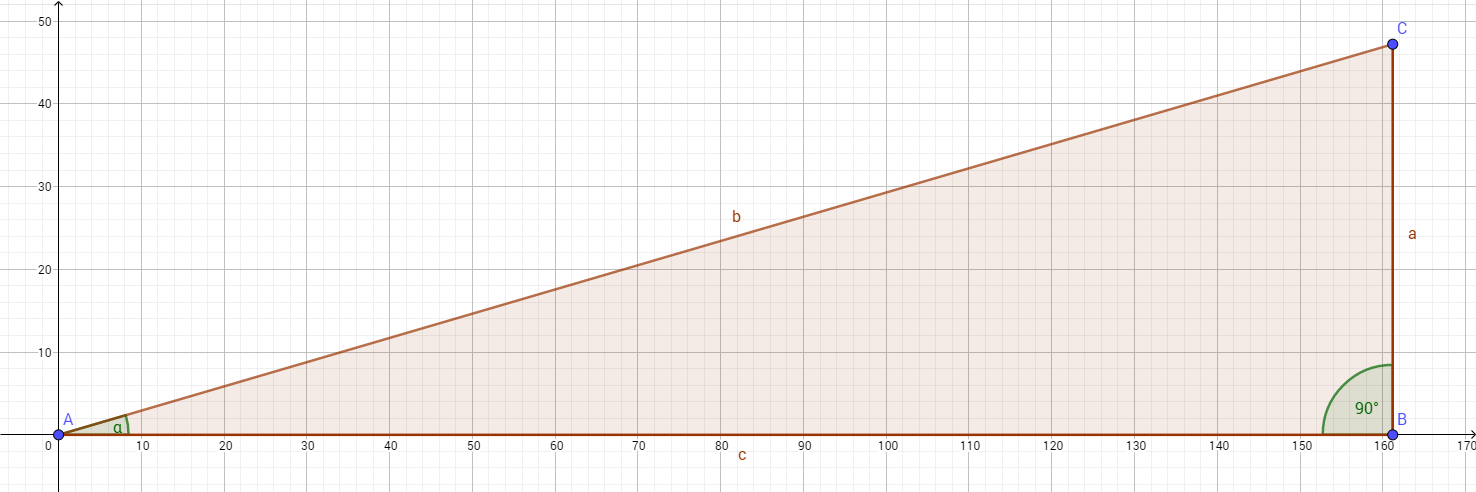
(c) Im Bild ist der obere Abschnitt der Baldwin Street vereinfacht als Dreieck dargestellt. Berechne die Straßenlänge $b$.

Aufgabe 3

Wir kennen nun die Länge der Straße $b$, die horizontale Entfernung $c$, die vertikale Entfernung $a$ und auch die Steigung – berechnet mit $\frac{a}{c}$. Für eine bessere Vorstellung wäre der Winkel interessant. Nutze das nachfolgende Applet oder eine maßstabsgerechte Zeichnung, um den Winkel näherungsweise zu bestimmen. Bei dem Applet kannst du einen Winkelmesser einblenden, ihn richtig positionieren und dann heranzoomen.

Zum Herunterladen: strasse.ggb

Noch mehr steile Straßen

Fassen wir die bisherigen Ergebnisse zum oberen Abschnitt der Baldwin Street zusammen: Man legt hier in horizontaler Richtung $c=161,2$ Meter zurück und dabei geht es $a=47,2$ Meter aufwärts. Die Straße ist $b=167,97$ Meter lang. Die Steigung beträgt dabei $29,28\%$ und der Steigungswinkel beträgt $\alpha=16,3°$.

Aufgabe 4

Im Rahmen eines Kunstprojekts soll nun ein Modell einer Straße mit demselben Steigungswinkel entstehen – allerdings mit einer horizontalen Länge von nur 2 Metern. Dafür braucht es ein Dreieck $A'B'C'$ mit den Seitenlängen $a'$, $b'$ und $c'$.

(a) Amir beginnt bereits, eine Zeichnung anzulegen. Mit der Seitenlänge $c'=2$ und dem Winkel $\alpha$ kann sie ein Dreieck zeichnen und dann die Seitenlängen $a′$ und $b′$ ablesen. Seine Freundin Birte meint, dass sie das auch einfach ausrechnen könne: Es gilt $\frac{a}{c} = \frac{a'}{c'}$ und damit $a'= \frac{a}{c} \cdot c' = \frac{47,2 }{161,2} \cdot 2 = \dots$ Erkläre, warum $\frac{a}{c} = \frac{a'}{c'}$ gilt. Du kannst hier sowohl inhaltlich als auch mit den Eigenschaften des Dreiecks argumentieren.

(b) Berechne auf diese Weise die Seitenlängen $a'$ und $b'$.

(c) Wie lang wäre eine Straße mit derselben Steigung, wenn man sich insgesamt 50 Meter nach oben bewegt?

(d) Wie viele Meter würde man sich in horizontaler und vertikaler Richtung bewegen, wenn man einen Kilometer lang auf einer so steilen Straße fährt?

Aufgabe 5

Du hast nun sowohl zeichnerisch als auch rechnerisch fehlende Größen eines Dreiecks bestimmt. Sammle Vorteile des rechnerischen Vorgehens.