o-mathe | Winkelfunktionen – Eine geometrische Sicht » Vertiefung

Vertiefung – Umkehrung der Winkelfunktionen

Kontext: Skipisten

Skipisten sind in verschiedene Klassen eingeteilt: Leichte Pisten (blau) haben ein Gefälle von maxmimal 25%. Rote Pisten haben ein Gefälle von maximal 40%. Schwarze Pisten liegen sogar über diesen 40%. Das Gefälle wird dabei komplett analog zur Steigung von Straßen berechnet.

Orientierungstafel mit Pistennummern in verschiedenen Schwierigkeitsgraden

Aufgabe 1: Mathematische Beschreibung

Hier ist eine Beispiel-Piste mit dem Neigungswinkel $\beta$ abgebildet. Die Piste selbst ist die Strecke $a$. Erkläre, wie man hier das Gefälle ausrechnet. Welcher Winkelfunktion entspricht das?

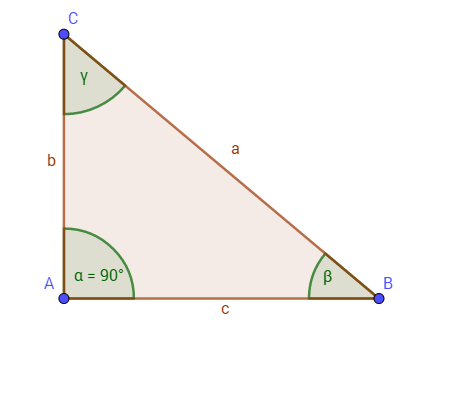
Dreieck mit eingezeichnetem Neigungswinkel

Das Gefälle berechnen

Verschiedene Skipisten in Schneehausen sollen ausgeschildert werden. Dafür muss für jede Piste das Gefälle bekannt sein, um die entsprechende Farbe herauszufinden.

Aufgabe 2: Gefälle berechnen

Berechne für die folgenden Pisten (Benennung wie in der Abbildung aus Aufgabe 1) das Gefälle in Prozent und entscheide, welche Farbe die Piste erhält. Achte auf einen nachvollziehbaren Rechenweg.

(a) Neigungswinkel $\beta = 12°$.

(b) Winkel $\gamma = 70°$.

(d) Die Piste ist $100$ m lang und hat einen Höhenunterschied von $38$ m. Achtung: Achte darauf, wirklich das Gefälle und nicht irgendetwas anderes auszurechnen.

Du bist vielleicht geneigt, hier einfach $38$ m durch $100$ m zu teilen. Aber das wäre nicht richtig; du brauchst die Länge der Seite $c$. Die bekommst du mit dem Satz des Pythagoras.

Andere Größen

Außer dem Gefälle in Prozent sind für die Gäste noch andere Größen interessant.

Aufgabe 3: Weitere Berechnungen

(a) In der Situation (a) von Aufgabe 2 beträgt $c = 200$ m. Berechne die anderen Größen des Dreiecks.

(b) In der Situation (b) von Aufgabe 2 beträgt $b = 20$ m. Berechne die anderen Größen des Dreiecks.

(c) Uns interessiert der Neigungswinkel $\beta$ zur Situation aus Aufgabe 2 (c). Erkläre, inwiefern sich diese Aufgabe von den anderen beiden Aufgabenteilen unterscheidet. Wieso lässt sich das nicht mit den bisher bekannten Mitteln berechnen?

Aufgabe 4: Wir bestimmen den Neigungswinkel

Löse das Problem aus Aufgabe 3 (c) mit dem nachfolgenden Applet. Bestimme also den Neigungswinkel, sodass das Gefälle $\frac{6}{20}=0,3=30$% beträgt.

Das Gefälle oder die Steigung entsprechen einer Winkelfunktion. Welcher? Stelle nun $\beta$ so ein, dass die entsprechende Winkelfunktion in etwa $0,3$ beträgt. Dann hast du den richtigen Winkel gefunden.

Zum Herunterladen: skipiste.ggb

Strukturierung

Wir interpretieren die Erkenntnisse von eben aus Sicht der Mathematik.

Aufgabe 5: Was bedeutet das mathematisch?

(a) Imke behauptet: „Nun haben wir also den Tangens umgekehrt.“ Was meint sie damit? Erkläre.

(b) Jayden meint, man kann mit dem Applet oben herausfinden, bei welchem Winkel $\beta$ gilt, dass $\sin(\beta)=0,38$ (das wäre die Situation aus Aufgabe 2d) oder wann $\cos(\beta)=0,9$. Kläre beide Fragen mit dem Applet.

(c) Imke hat im Mathematik-Unterricht aufgepasst: „Man kann nicht jede Funktion umkehren.“ Welches Gegenbeispiel kennst du?

(d) Jayden erklärt: „Wenn man den Sinus umkehren kann, dann darf es nicht ... geben.“ Ergänze den fehlenden Teil der Erklärung.

Wir betrachten ein konkretes Beispiel. Du kannst mit dem Taschenrechner herausfinden, dass $\sin(30°)=0,5$. Damit der Sinus nun umkehrbar ist, darf es eine Sache nicht geben. Welche?

(e) Imke hat im Applet ein Argument dafür gefunden, dass die Winkelfunktionen umkehrbar sind: „Wenn ich den Winkel vergrößere, dann wird der Sinus immer ..., der Kosinus immer ... und der Tangens immer .... Also gibt es keine zwei Winkel, bei denen z.B. der Sinus denselben Wert hat.“ Ergänze die fehlenden Teile und vollziehe das Argument nach.

(f) Suche auf deinem Taschenrechner einen Weg, um die drei Winkelfunktionen umzukehren.

Mathematische Präzisierung

Die Überlegungen der vorherigen Aufgabe machen es plausibel, dass man die Winkelfunktionen umkehren kann. Ein mathematischer Beweis ist das aber noch nicht. Diesen lassen wir an dieser Stelle aus. Dennoch halten wir ohne Beweis die wichtige Erkenntnis fest:

Satz: Die Winkelfunktionen Sinus, Kosinus und Tangens im rechtwinkligen Dreieck sind umkehrbar. Man findet also für ein zulässiges Seitenverhältnis $q$ einen eindeutigen Winkel $\alpha$ zwischen $0°$ und $90°$, sodass $\sin(\alpha)=q$ bzw. $\cos(\alpha)=q$ bzw. $\tan(\alpha)=q$

Wann ein Seitenverhältnis „zulässig“ ist, müssen wir noch klären.

Da die Winkelfunktionen umkehrbar sind, können wir ihren Umkehrungen auch Namen geben: Sie werden Arkussinus, Arkuskosinus und Arkustangens genannt. Man schreibt dafür $\arcsin(\alpha)$, $\arccos(\alpha)$ bzw. $\arctan(\alpha)$.

Es gibt eine andere verbreitete Schreibweise für die drei „Arkusfunktionen“, die vor allem auf Taschenrechnern verbreitet ist: $\sin^{-1}(\alpha)$, $\cos^{-1}(\alpha)$ und $\tan^{-1}(\alpha)$. Der Ausdruck „ ☐$^{-1}$“ ist dabei eine Schreibweise, um auf die Umkehrfunktion hinzuweisen. Es bedeutet nicht, dass hier ein Kehrwert gebildet oder mit $-1$ potenziert wird. Aufgrund dieser möglichen Verwirrung, verwenden wir die „Arkus“-Schreibweise.

Aufgabe 6: Das Wichtigste notieren

Ergänze deine Zusammenfassung aus der Strukturierung zu Winkelfunktionen um folgende weiteren Punkte:

Umkehrung: Erkläre kurz, wozu die drei Umkehrfunktionen genutzt werden: Welche Figur wird betrachtet? Welche Größen sind bekannt? Welche Größen sind unbekannt?
Umkehrfunktionen: Führe die drei Umkehrfunktionen mit ihrer Schreibweise auf.

Quellen

[1]: signes routiers ski madonna di campiglio italie - Urheber: Abxbay - Lizenz: Creative Commons BY-SA 3.0