Zusammenfassung – Lagebeziehungen bei Geraden
Gegenseitige Lage von Geraden im 3D-Raum
Das folgende Applet zeigt 4 Geraden, die unterschiedlich zueinander liegen.
Zum Herunterladen: geraden.ggb
Definition
Zur Beschreibung von Lagebeziehungen nutzen wir die folgenden Fachbegriffe:
- Zwei Geraden schneiden sich in genau einem Punkt, wenn es genau einen Punkt gibt, der auf beiden Geraden liegt. Im Beispiel $g$ und $h$.
- Zwei Geraden sind identisch genau dann, wenn sie in allen Punkten übereinstimmen. Im Beispiel $h$ und $j$.
- Zwei Geraden sind (echt) parallel genau dann, wenn sie parallel, aber nicht identisch sind. Im Beispiel $g$ und $i$. Man nutzt den Zusatz „echt“, um klarzustellen, dass die Geraden nicht identisch sind.
- Zwei Geraden sind windschief genau dann, wenn sie nicht parallel zueinander sind, sich aber auch nicht schneiden. Im Beispiel $h$ und $i$.
Diese vier Begriffe decken alle möglichen Lagebeziehungen ab:
Satz
Zwei Geraden im 3D-Raum stehen immer in genau einer der obengenannten Lagebeziehungen.
Dieser Satz ist anschaulich klar. Er besagt zum einen z. B., dass zwei Geraden nicht gleichzeitig parallel und schneidend sein können. Zum anderen besagt er aber auch, dass immer eine Lagebeziehung zutrifft und zwei Geraden nicht etwa in genau zwei Punkten übereinstimmen können. Auf einen Beweis verzichten wir an dieser Stelle, weil die Aussage anschaulich klar sein sollte.
Ein Algorithmus zur Untersuchung der Lagebeziehungen
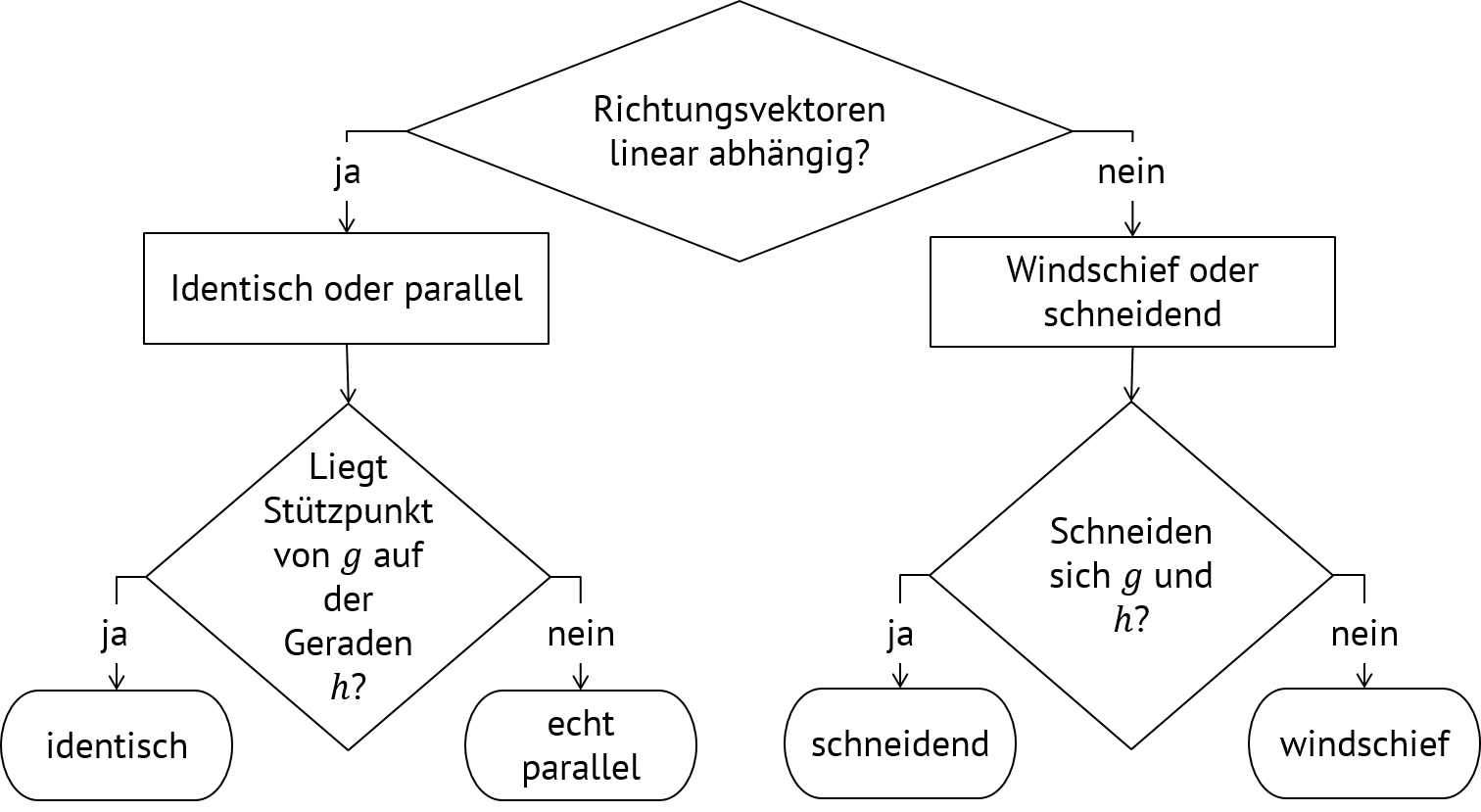
Man kann Lagebeziehungen mit diesem Algorithmus untersuchen.
Er verwendet zum einen Sätze über den Zusammenhang von Lagebeziehungen und den Bestandteilen einer Geradengleichung (siehe unten) und zum anderen bringt er die Untersuchungsschritte in eine geschickte Reihenfolge, um sich z.B. die aufwendige Schnittpunktbestimmung in zwei Fällen zu sparen.Identische Geraden
Zum Herunterladen: geraden_h_j.ggb
Satz
Wenn die Richtungsvektoren der beiden Geraden linear abhängig sind und zusätzlich der Punkt zum Stützvektor einer Geraden auch auf der anderen Geraden liegt, dann sind die beiden Geraden identisch.
Beispiel:
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ (mit $s \in \mathbb{R}$)
$j: \vec{x} = \left(\begin{array}{c} -4 \\ -3 \\ 2 \end{array}\right) + k \cdot \left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array}\right)$ (mit $k \in \mathbb{R}$)
Lösungen ein-/ausblenden
Hier gilt:
- $(-1) \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right) = \left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array}\right)$. Die Richtungsvektoren von $h$ und $j$ sind also linear abhängig.
- $\left(\begin{array}{c} -4 \\ -3 \\ 2 \end{array}\right) + 4 \cdot \left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array}\right) = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right)$. Der Stützpunkt $(4|1|2)$ von $h$ liegt also auch auf $j$.
Also sind die Geraden identisch.
Echt parallele Geraden
Zum Herunterladen: geraden_g_i.ggb
Satz
Wenn die Richtungsvektoren der beiden Geraden linear abhängig sind und zusätzlich der Punkt zum Stützvektor einer Geraden nicht auf der anderen Geraden liegt, dann sind die beiden Geraden echt parallel.
Beispiel:
$g: \vec{x} = \left(\begin{array}{c} 2 \\ -5 \\ 2 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right)$ (mit $t \in \mathbb{R}$)
$i: \vec{x} = \left(\begin{array}{c} -2 \\ 4 \\ 4 \end{array}\right) + r \cdot \left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$ (mit $r \in \mathbb{R}$)
Lösungen ein-/ausblenden
Hier gilt:
- $(-1) \cdot \left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right) = \left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$. Die Richtungsvektoren von $g$ und $i$ sind also linear abhängig.
- Der Stützpunkt $(2|-5|2)$ von $g$ liegt nicht auf $i$, da alle Punkte auf $i$ die $x_3$-Koordinate $4$ haben. Dieses Ergebnis erhält man auch leicht aus einer Punktprobe.
Also sind die Geraden echt parallel.
Sich schneidende Geraden
Zum Herunterladen: geraden_g_h.ggb
Satz
Wenn die Richtungsvektoren der beiden Geraden nicht linear abhängig sind und die Geraden zusätzlich einen gemeinsamen Punkt haben, dann schneiden sich die beiden Geraden in einem Punkt.
Beispiel:
$g: \vec{x} = \left(\begin{array}{c} 2 \\ -5 \\ 2 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right)$ (mit $t \in \mathbb{R}$)
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ (mit $s \in \mathbb{R}$)
Lösungen ein-/ausblenden
Hier gilt:
- Die Richtungsvektoren $\left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right)$ und $\left(\begin{array}{c} -2 \\ 1 \\ 0 \end{array}\right)$ sind nicht linear abhängig.
- Der Punkt $(0|-1|2)$ liegt auf $g$ (mit $t = 2$) und auf $h$ (mit $s = 2$). Es gibt also einen gemeinsamen Punkt. Um $t$ und $s$ passend auszurechnen, nutzt man normalerweise eine Schnittpunktberechnung.
Also schneiden sich die Geraden in genau einem Punkt.
Windschiefe Geraden
Zum Herunterladen: geraden_h_i.ggb
Satz
Wenn die Richtungsvektoren der beiden Geraden nicht linear abhängig sind und die Geraden keinen gemeinsamen Punkt haben, dann sich die beiden Geraden windschief.
Beispiel:
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 1 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ (mit $s \in \mathbb{R}$)
$i: \vec{x} = \left(\begin{array}{c} -2 \\ 4 \\ 4 \end{array}\right) + r \cdot \left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$ (mit $r \in \mathbb{R}$)
Lösungen ein-/ausblenden
Hier gilt:
- Die Richtungsvektoren $\left(\begin{array}{c} -2 \\ -1 \\ 0 \end{array}\right)$ und $\left(\begin{array}{c} 1 \\ -2 \\ 0 \end{array}\right)$ sind nicht linear abhängig.
- Es kann keine gemeinsamen Punkte geben, weil alle Punkte von $h$ die $x_3$-Koordinate $2$ haben, während alle Punkte von $i$ die $x_3$-Koordinate $4$ haben. Das war hier besonders einfach, weil eine Koordinate bei beiden Gleichungen unverändert blieb. In schwierigeren Fällen bleibt nur eine Schnittpunktberechnung.
Also sind die Geraden windschief.
Quellen
- [1]: Flussdiagramm zur Untersuchung der Lagebeziehungen - Urheber: FR - Lizenz: inf-schule.de