Zusammenfassung – Spurpunkte von Geraden
Visualisierung von Geraden im 3D-Raum
Bei der Verdeutlichung der Lage von Geraden im 3D-Raum helfen die sogenannten Spurpunkte.
Zusammenfassung – Spurpunkte von Geraden: spurpunkte3.ggb
Die Spurpunkte einer Geraden sind die Schnittpunkte einer Geraden mit den Koordinatenebenen.
- Der Spurpunkt $S_{12}$ ist der Schnittpunkt der Geraden mit der $x_1$-$x_2$-Ebene (die durch die $x_1$-Achse und die $x_2$-Achse festgelegt ist).
- Der Spurpunkt $S_{13}$ ist der Schnittpunkt der Geraden mit der $x_1$-$x_3$-Ebene (die durch die $x_1$-Achse und die $x_3$-Achse festgelegt ist).
- Der Spurpunkt $S_{23}$ ist der Schnittpunkt der Geraden mit der $x_2$-$x_3$-Ebene (die durch die $x_2$-Achse und die $x_3$-Achse festgelegt ist).
Berechnung der Spurpunkte
Wir betrachten die folgende Gerade.
$g: \vec{x} = \left(\begin{array}{c} 1 \\ 1.5 \\ 1.5 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 1.5 \\ 0.5 \end{array}\right)$ (mit $t \in \mathbb{R}$)
Beispiel: Bestimmung von $S_{12}$
Der Punkt $S_{12}$ liegt in der $x_1$-$x_2$-Ebene. Die $x_3$-Koordinate dieses Punktes muss also $0$ sein. $S_{12}$ hat also die Koordinaten $S_{12}(x|y|0)$ mit noch zu bestimmenden Koordinaten $x$ und $y$.
Da der Punkt $S_{12}$ auf der Geraden $g$ liegt, muss folgende Bedingung erfüllt sein:
$\left(\begin{array}{c} x \\ y \\ 0 \end{array}\right) = \left(\begin{array}{c} 1 \\ 1.5 \\ 1.5 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 1.5 \\ 0.5 \end{array}\right)$
Durch zeilenweises Auswerten ergibt sich das folgende lineare Gleichungssystem (LGS):
$\begin{array}{ccccc} [1] &\quad x & = & 1 & - & t \\ [2] &\quad y & = & 1.5 & + & 1.5t \\ [3] &\quad 0 & = & 1.5 & + & 0.5t \end{array}$
Auflösen von [3] ergibt: $t = -3$
Einsetzen von $t = -3$ in [1] und Auflösen von [1] ergibt: $x = 4$
Einsetzen von $t = -3$ in [2] und Auflösen von [2] ergibt: $y = -3$
Ergebnis: $S_{12}$ hat also die Koordinaten $S_{12}(4| -3| 0)$.
Beispiel: Bestimmung von $S_{13}$
Bei der Bestimmung von $S_{13}$ geht man analog vor. $S_{13}$ liegt in der $x_1$-$x_3$-Ebene. Die $x_2$-Koordinate dieses Punktes muss also $0$ sein. $S_{13}$ hat also die Koordinaten $S_{13}(x|0|z)$ mit noch zu bestimmenden Koordinaten $x$ und $z$.
Da der Punkt $S_{13}$ auf der Geraden $g$ liegt, muss folgende Bedingung erfüllt sein:
$\left(\begin{array}{c} x \\ 0 \\ z \end{array}\right) = \left(\begin{array}{c} 1 \\ 1.5 \\ 1.5 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 1.5 \\ 0.5 \end{array}\right)$
Durch zeilenweises Auswerten ergibt sich das folgende lineare Gleichungssystem (LGS):
$\begin{array}{ccccc} [1] &\quad x & = & 1 & - & t \\ [2] &\quad 0 & = & 1.5 & + & 1.5t \\ [3] &\quad z & = & 1.5 & + & 0.5t \end{array}$
Auflösen von [2] ergibt: $t = -1$
Einsetzen von $t = -1$ in [1] und Auflösen von [1] ergibt: $x = 2$
Einsetzen von $t = -1$ in [3] und Auflösen von [3] ergibt: $z = 1$
Ergebnis: $S_{13}$ hat also die Koordinaten $S_{13}(2, 0, 1)$.
Beispiel: Bestimmung von $S_{23}$
$S_{23}$ liegt in der $x_2$-$x_3$-Ebene. Die $x_1$-Koordinate dieses Punktes muss also $0$ sein. $S_{23}$ hat also die Koordinaten $S_{23}(0|y|z)$. mit noch zu bestimmenden Koordinaten $x$ und $z$.
Da der Punkt $S_{23}$ auf der Geraden $g$ liegt, muss folgende Bedingung erfüllt sein:
$\left(\begin{array}{c} 0 \\ y \\ z \end{array}\right) = \left(\begin{array}{c} 1 \\ 1.5 \\ 1.5 \end{array}\right) + t \cdot \left(\begin{array}{c} -1 \\ 1.5 \\ 0.5 \end{array}\right)$
Durch zeilenweises Auswerten ergibt sich das folgende lineare Gleichungssystem (LGS):
$\begin{array}{ccccc} [1] &\quad 0 & = & 1 & - & t \\ [2] &\quad y & = & 1.5 & + & 1.5t \\ [3] &\quad z & = & 1.5 & + & 0.5t \end{array}$
Auflösen von [1] ergibt: $t = 1$
Einsetzen von $t = 1$ in [2] und Auflösen von [2] ergibt: $y = 3$
Einsetzen von $t = 1$ in [3] und Auflösen von [3] ergibt: $z = 2$
Ergebnis: $S_{23}$ hat also die Koordinaten $S_{13}(0, 3, 2)$.
Sonderfälle – Anzahl der Spurpunkte
Die Anzahl der Spurpunkte hängt von der Lage der Geraden ab.
| Lage der Gerade | Spurpunkte |
|---|---|
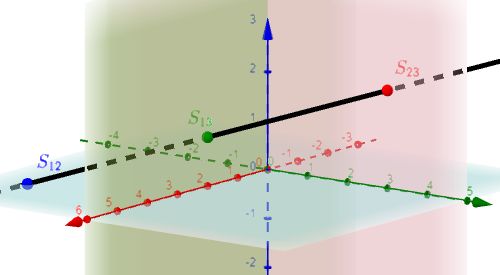 |
$S_{12}$, $S_{13}$, $S_{23}$ |
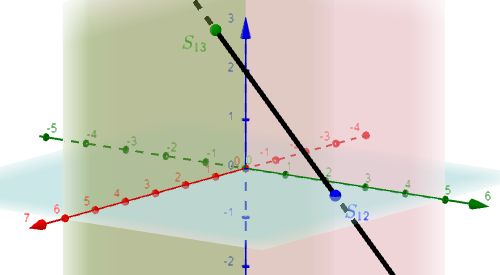 |
$S_{12}$, $S_{13}$ |
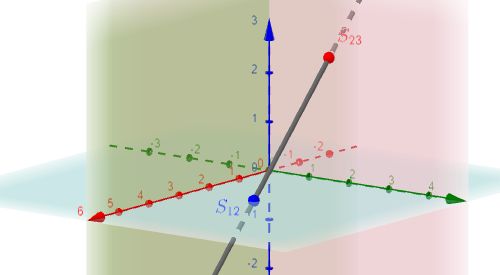 |
$S_{12}$, $S_{23}$ |
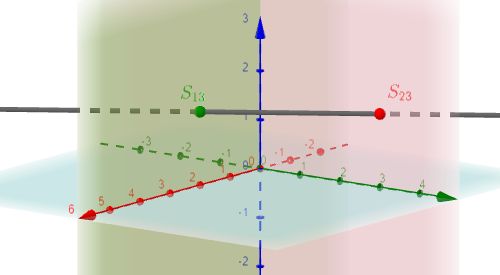 |
$S_{13}$, $S_{23}$ |
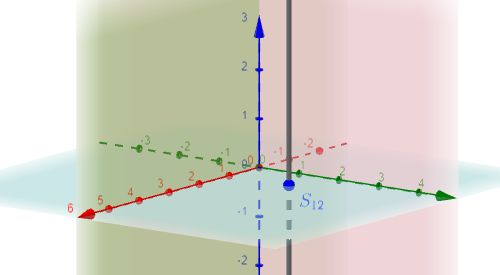 |
$S_{12}$ |
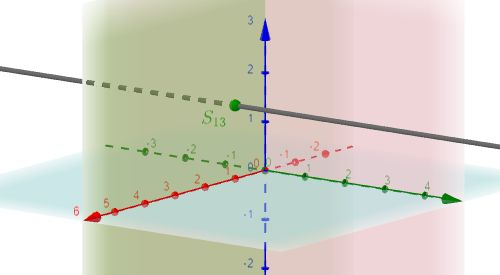 |
$S_{13}$ |
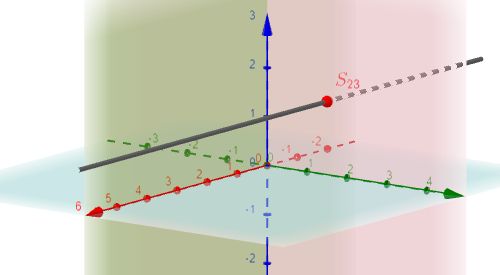 |
$S_{23}$ |

